Car Jump (basic)

Leave a Comment / Physics / By /

Concepts addressed: Projectile motion skills
Grade level: 11th.
An Advanced version of Car Jump is also available.

Scenario:

A Hollywood production has called you in as a physics expert. They are filming the latest Marvel movie and they need a shot of a car flying off a ramp and landing safely on the ground. To do this they use very expensive miniatures of the real car. To protect the replica (for future shots and repetitions of the jump stunt), they have a landing pad that has an area slightly larger than the replica they will launch; so we need to a precision of 3 decimal places.

The ramp from which the car will launch is angled at 30 degrees from the horizontal. The studio has already figured out that the speed of the model will be 3.0 m/s at launch.

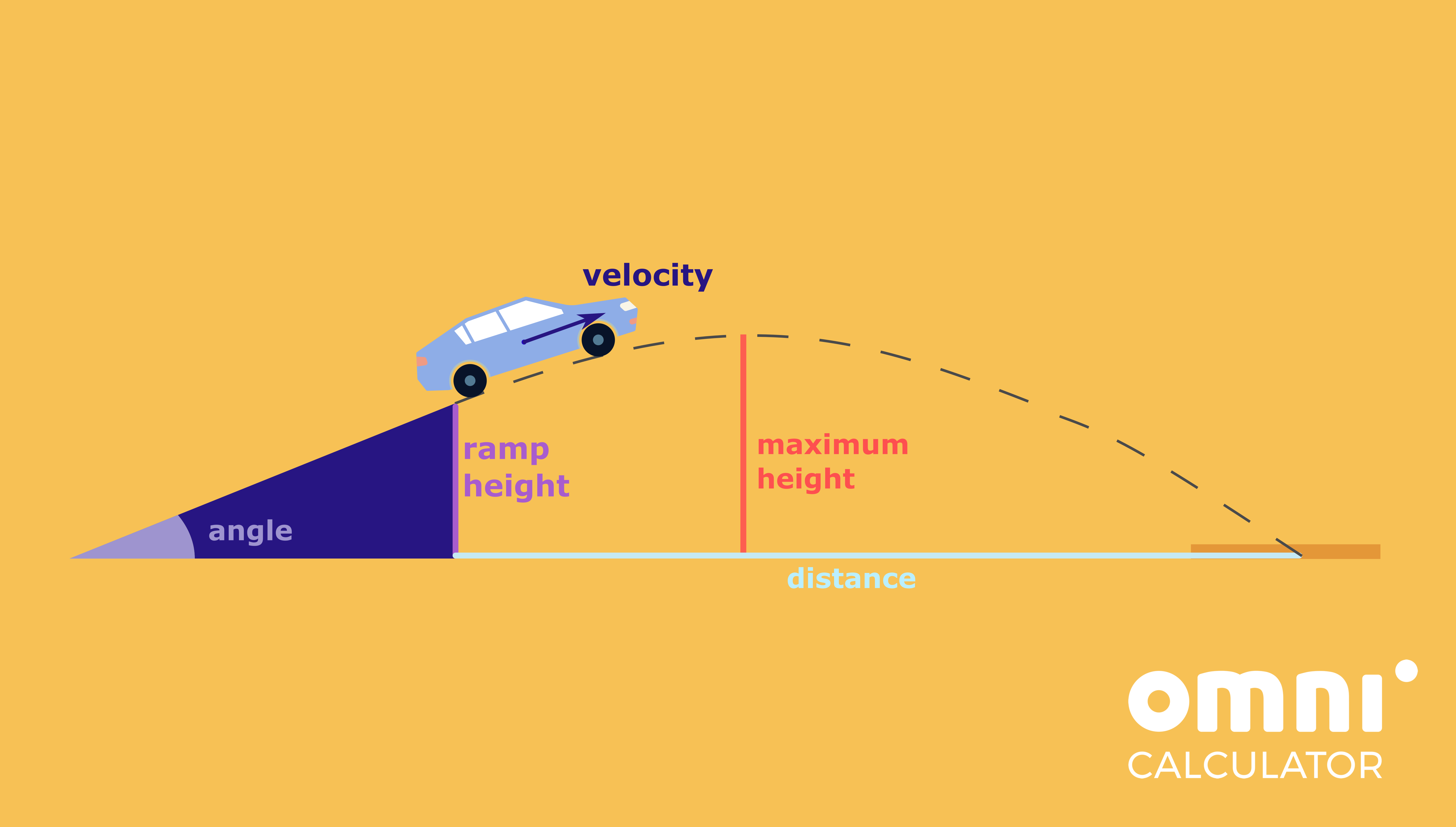
  1. Knowing that the ramp is 50.0 cm above the ground when the car leaves it, how long will the model car be in the air for?
  2. How far will the car travel in the horizontal direction?
  3. What will be the maximum height of the car (measured from the ground) during the jump?

Useful calculators:

Question 1 hints:

Hint 1
You can ignore air resistance for this and all questions.
Hint 2
You don’t need to think about the horizontal movement, only how long it will take the car to reach the ground.
Hint 3
In the vertical direction the motion of the car is only affected by the Earth’s gravity.

Question 2 hints:

Hint 1
This time we only care about the movement in the horizontal direction.
Hint 2
The car moves forward at a constant speed.
Hint 3
We only care about the car moving forward while it is in the air, so Question 1 will help you.

Question 3 hints:

Hint 1
Once again, we’re focused on the vertical movement only.
Hint 2
At the highest point of the jump, the speed is zero as it has been completely counteracted by the acceleration due to gravity.
Hint 3
First you need to calculate the time it takes the car to reach the highest point, and then you can compute the height at such a point.

Solutions :

Question 1
The result is that the car will fly for 0.51 seconds.
Question 2
The car will travel 1.3 m horizontally during its flight.
Question 3
The car will reach a maximum height of 0.62 m.

Step-by-Step Solutions :

Question 1
This a projectile motion problem. We can break down the movement into its x (horizontal) and y (vertical) components.
The car will stop flying when it reached the ground, which can be written as y(t) = 0. We can find t by solving the quadratic equation:
y(t) = (1/2) * a * t2 + vy * t + y(0)
Substituting in the values we get: 0 = (1/2) * (-g) * t2 + v * sin(30º) * t + 50 cm,
where v is the speed at the moment of takeoff, g is the acceleration of gravity (negative since it points towards the center of the Earth).
Using the Quadratic Formula calculator  we find that the car will fly for 0.51 seconds.
Question 2
Now that we know the time the car is in the air for, we can calculate the horizontal distance travelled. Since there is no horizontal acceleration (as we neglect air resistance), all we need to do is apply the speed formula:
x(t) = vx*t = v * cos(θ) * t
Substituting t for the time of flight: x = 3.0 m/s * cos(30º) * 0.51 s
The car will travel 1.317 m horizontally during its flight.
Question 3
The car will be at its highest when it does not have any vertical speed, vy = 0. (right before it starts to fall).
We know that the equation for speed at any time is:
vy(t) = a * t + vy(0) => t = [vy(t) – vy(0)] / a = [0 – v(0) * sin(30º)] / (-g)
Substituting in the values we already know, we find that the car will reach a maximum height of 0.62 m.

Dear teacher! We're in an early stage of this project. Our main objective right now is to learn how to make scenarios that best suit your needs. Please use the comment box below to tell us:
  • Is the difficulty level right for your class?
  • How would you use it in class?
  • How would you improve this scenario?
  • A bonus: what are you teaching next week? We'd love to prepare a scenario for you 🙂

Leave a Reply

Your email address will not be published.