Concepts addressed: refraction, geometric and trigonometric analysis
Grade level: 10th.
Scenario:

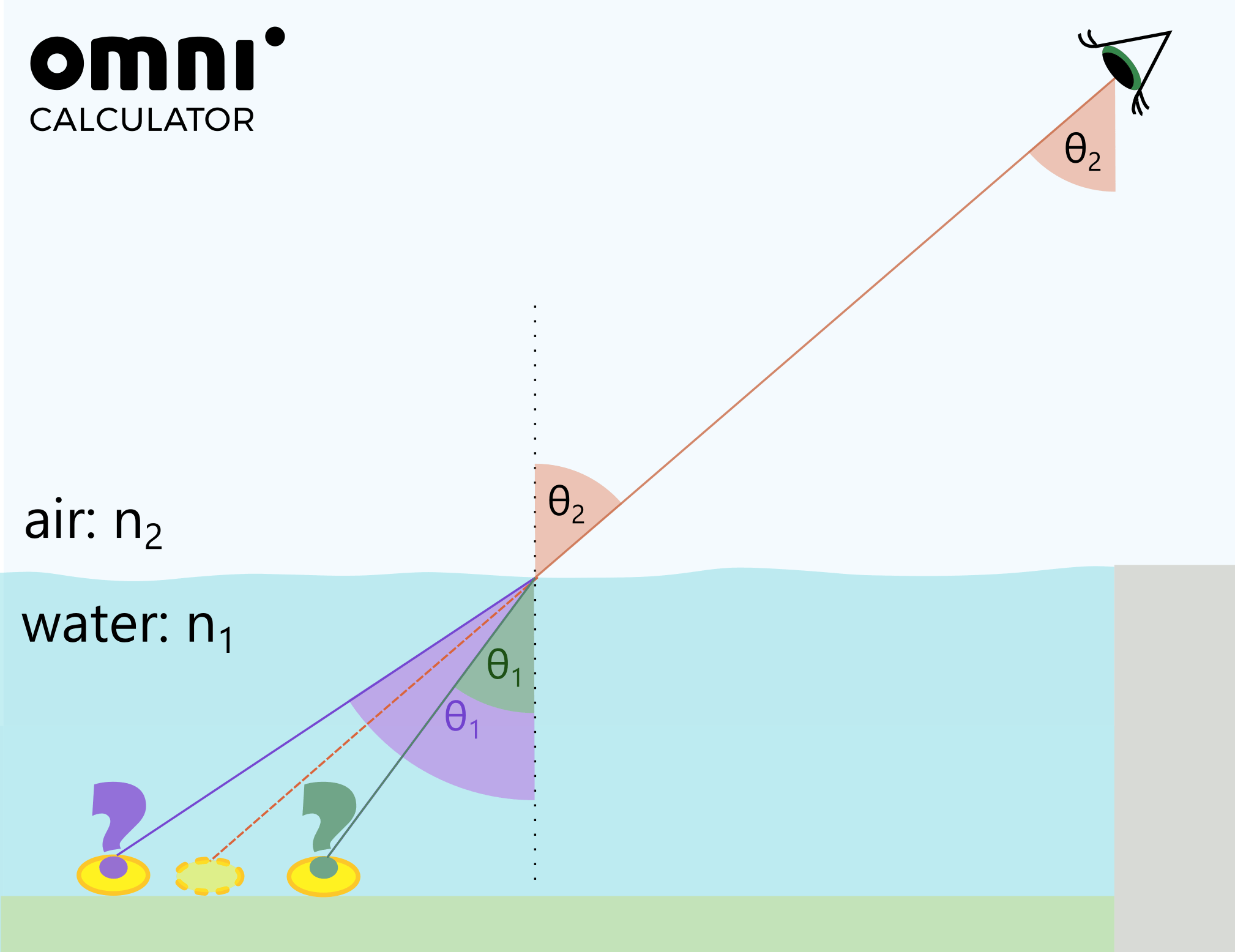
A week ago, while walking through the park, I stood by the pond as I always do. While looking down at the water, I noticed something shiny – a golden coin! From where I stood, it seemed to be 1.50 m meters from the shore. I know I can only reach 1.00 m horizontally into the pond without getting my feet wet, but I also know that due to the refraction of light, the coin is not where it appears to be. As you can see in the image, I was standing on the edge of the pond, and my eyes are 1.70 m above the level of the water. The lake has a constant depth of 0.50 m deep.
Questions:
- Is the coin closer or further from me than it seems?
- Can I reach the coin without getting my feet wet?
Data:
Refraction index air: n2 = 1
Refraction index water: n1 = 1.33
Useful calculators:
- Right triangle calculator – https://www.omnicalculator.com/math/right-triangle-side-angle
- Snell’s Law calculator – https://www.omnicalculator.com/physics/snells-law
- Complementary angles calculator – https://www.omnicalculator.com/math/complementary-angles
Question 1 hints:
Question 2 hints:
See calculators. Solutions :
Step-by-Step solutions :
n1 * sin(θ1) = n2 * sin(θ2) => 1 * sin(θ1) = 1.33 * sin(θ2)
For the equality to hold, sin(θ1) > sin(θ2), and since both angles are smaller than 90º, θ1 > θ2 has to be true.
Look at the drawing. It means that the coin will be closer than it appears to be when I am looking from outside the water.
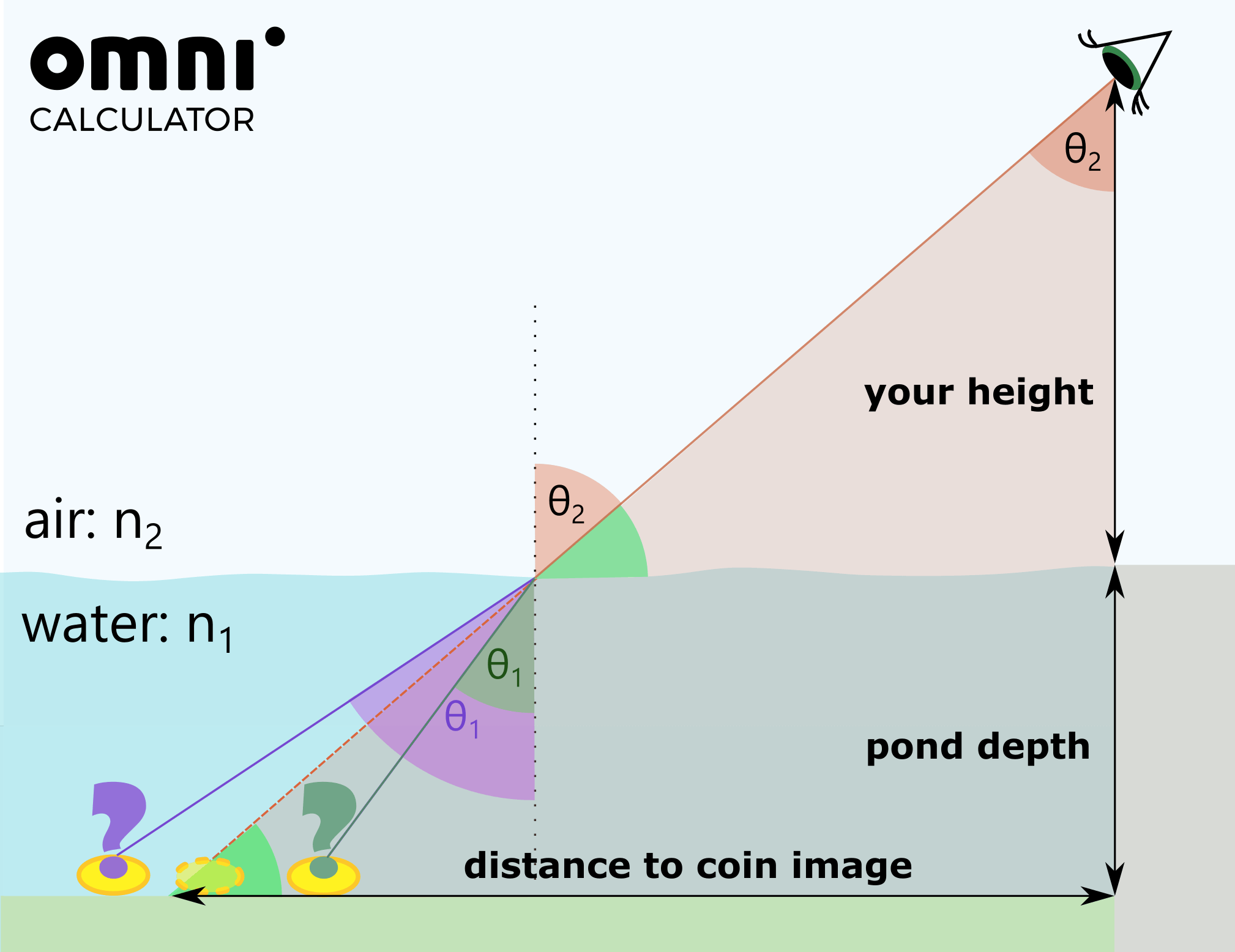
The first one is a triangle with hypotenuse going from my eyes to the image of the coin in the water. The other sides are known (my height plus the depth of the pond and the horizontal distance to the coin).
Using the Right triangle calculator, we can see that the angle I am looking at the coin with respect to the horizontal is: 56º
This is the same angle between my line of sight and the surface of the water. θ1 is, therefore, 90º – 56º = 34º
So, using the Snell’s Law calculator, we find θ2: 1 * sin (34º) = 1.33 * sin (θ1) => θ2 = 25º
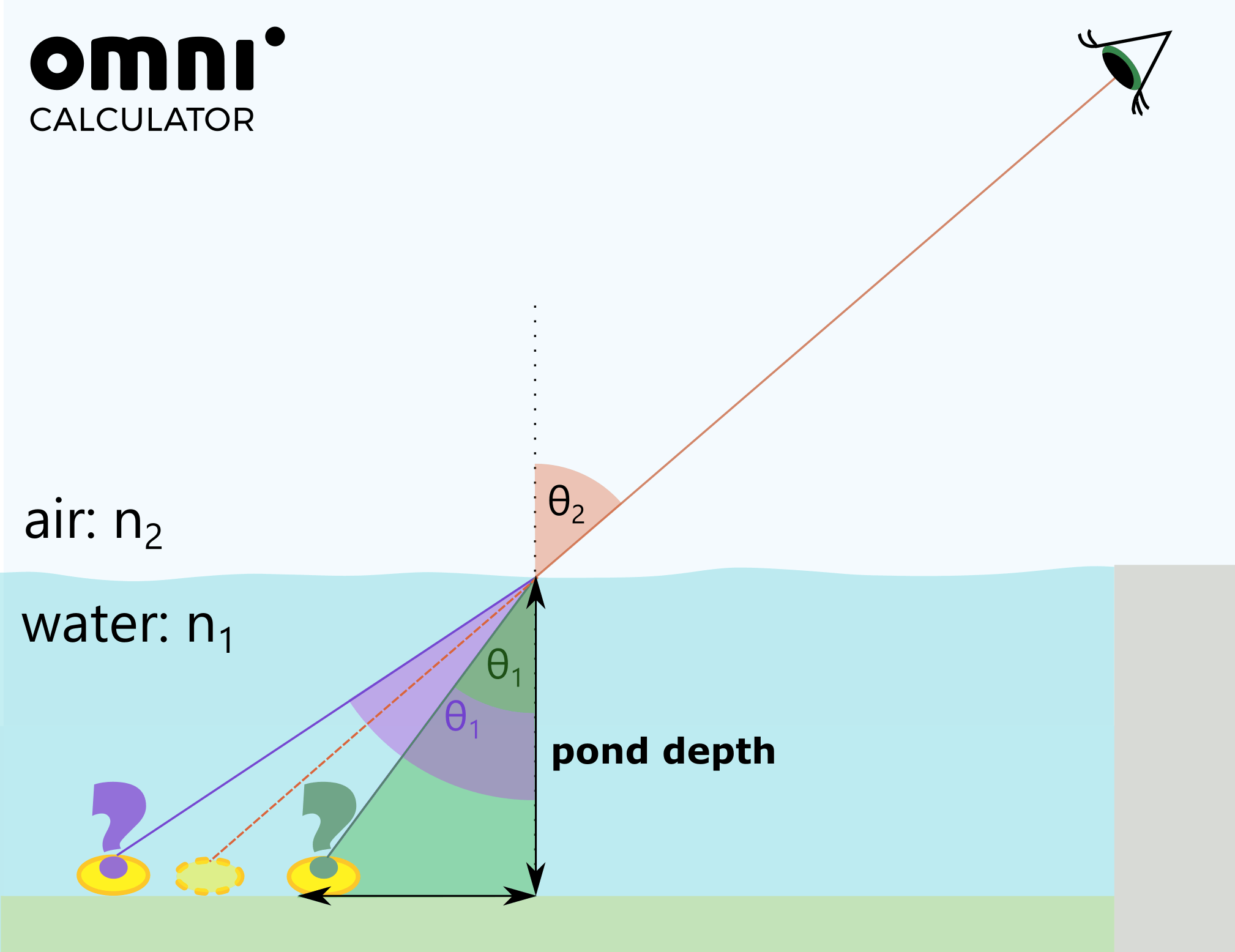
This leaves us with another triangle, where the hypotenuse goes from the point my line of sight intersects water to the coin, with height being the depth of the water. We know one angle is 25º and the other is
90º – 25º = 65º
This will let us find the horizontal distance from the normal to the coin, which is 23 cm. We know the horizontal distance from me to the normal from the first triangle we constructed; it is 1.2 m
Adding both horizontal distances, we find the distance to the coin: 1.2 m + 0.23 m = 1.4 m. So I will not able to reach the coin.
Thank you so much for making an interesting scenario. This will be a good challenge for most of my 14-18 year old students.I added these instructions:
CORRECTION!! The eye height above the water is 1.70 meters.
The apparent position of the doubloon is 1.5 m horizontally along the pond bottom, NOT the point on the surface where I “see” the image.
Use the SI units and Ignore all the values given in British Units.
Take a Snip/Picture and Draw the detailed numerical givens and your findings on the Sketch. OR make your own sketch making it closer to the realistic proportions (that the numbers imply).
Need Hints, Send me a message.
Submit the attached Report of your results, including every numerical value that you find or calculate.
Please also include a comment about your experience with this…what did you think?.
I am puzzled by the numerical answer, since my calculations do not come out to that value, using either the 1.70 cm nor 1.70 m and the precision of the answer exceeds the precision of the measurements.
Next I will be presenting Optics with mirrors and lenses, image position, ray tracing, some focal point calculations. Review of rotation and gravitation concepts and problems.Then a review of all mechanics.
In chemistry it will be balancing reactions, gas properties and affects of changes in temperature, pressure and volume, as well as Use of the Henderson-Hasselbalch equation and the Small-x approximation for solving equilibrium problems when Kc is either very small or very large.
Thank you for this sort of work.
Ah, good work. You already took care of the issues I noticed, and now the 0.50 m depth is perfectly, and appropriately added to the 1.70 m above the water giving me a chance to explain, and re-emphasize, to my students how ADDING measured values differs from the sig fig rules for multiplication and division. Yay!
Thank you so much for this, and your previous comment. We love constructive feedback!
I will try to make a nice scenario related to optics this week and hope it will be useful for you and your students… stay tuned!
Hi Alvaro, I especially like that your character by the pond is swarthy and that students of many origins might recognize someone who looks a bit like them doing science.
Today one of my students told me about a confusion. For some reason this student thought that the “eye” was leaning out beyond the edge of the pond, and thought that the horizontal distance of that extension over the water was missing, but critical information.
I made sure the entire class knew that the eye was meant to be directly above the water’s edge. It is nice, and sometimes maddening, to see how young folks can see things in our presented questions that we did not intend.
Kids often point out my errors (I celebrate this by awarding extra credit for doing this with at least a modicum of politeness) and little kids have no trouble telling adults that they know about errors.
I just looked at my prior message, and noticed that I did not make it clear where my instructions to students ended and my own comments continued. I believe that you and your team realized that my instructions ended with “what did you think?”. I never told my students about my confusion with the answer posted on your site at that time.
No great hurry on that new scenario…I will be able to use it until May 31, or next Autumn.
Bruce
Thanks again for your comment!
That is actually a good point, I would’ve never thought about it, but I can see how that’s confusing. Kids’ feedback is really something else, I love your approach to it!
We have updated the image and I hope it’s more clear now for your student.
We aim to have the scenario ready in about 2 weeks, to have some buffer.
Thank you again for your feedback!