Concepts addressed: Projectile motion Grade level: 12th. An easier version of Car Jump is also available.
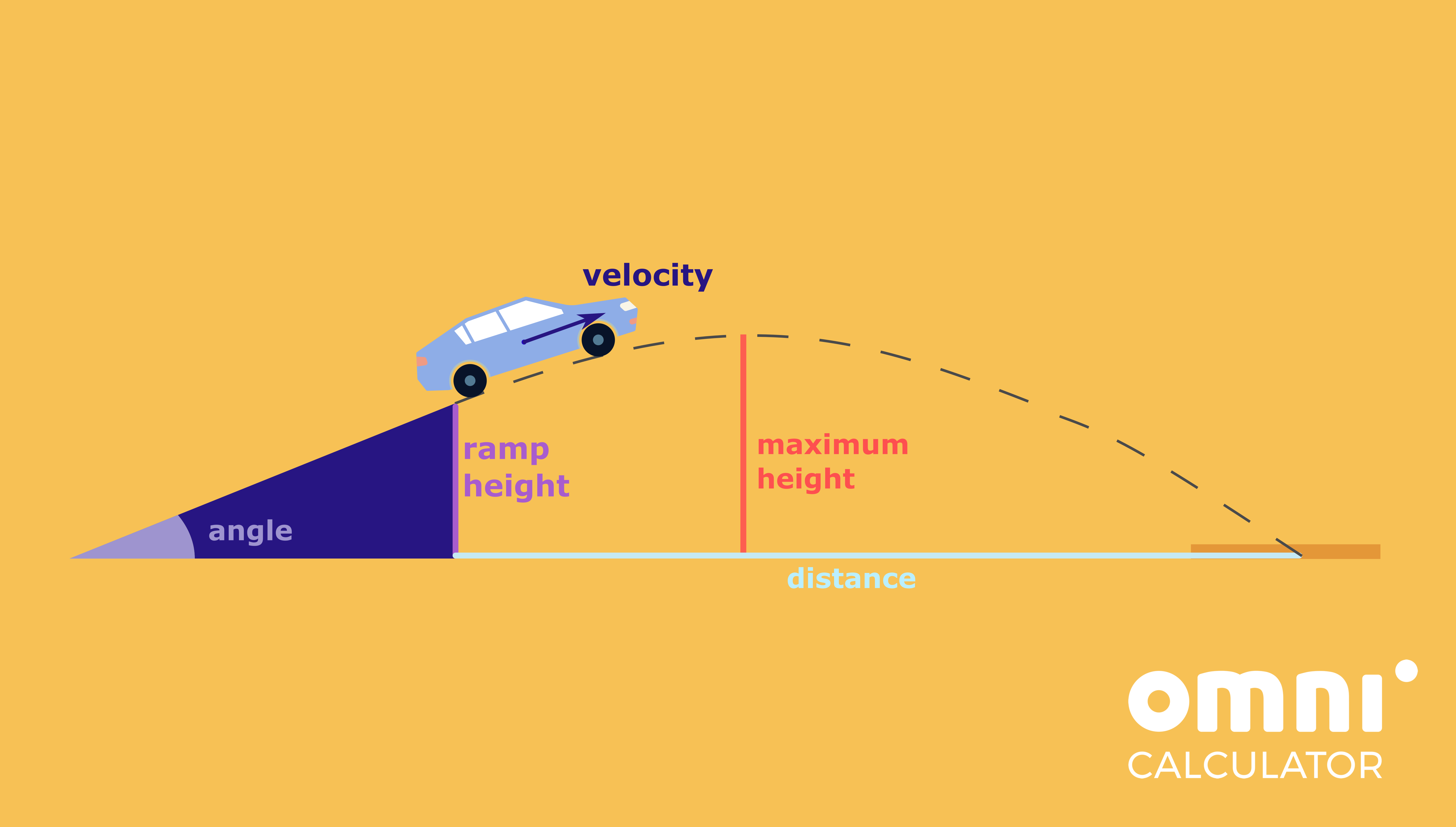
Scenario: A Hollywood production has called you in as a physics expert. They are filming the latest Marvel movie and they need a shot of a car flying off a ramp and landing safely on the ground. To do this they use very expensive miniatures of the real car. To protect the replica (for future shots and repetitions of the jump stunt), they have a landing pad that is 50% longer than the replica they will launch.
The ramp from which the car will launch is angled at 35 degrees. You can use your school’s lab equipment (low friction carts and pasco tracks) to recreate the launch and find a way of measuring the speed of the car. You are not allowed to launch the car before you have done your calculations and placed the landing pad.
Develop a way to measure the speed of the car consistently.
Use the previously measured value to predict where the car will land. Assume that the highest point of the ramp is 20.0 cm above the ground.
Can you come up with an expression that predicts where the landing pad should be as a function of the height of the ramp?
Recreate the stunt using the tools you have. You can use a foam rectangle as the landing pad.
Start by defining a set of points between which you can assume the speed is constant. You need to consistently measure the time between those points.
Hint 2
The set of points needs to be as close as possible to the end of the ramp. Knowing the distance and time between them you can get the speed.
Question 2 hints:
Hint 1
You can ignore air resistance.
Hint 2
In a projectile problem you can separate the horizontal and vertical components of the movement.
Hint 3
Use the height to calculate the total time of flight. Use that time to calculate the distance traveled in the X-direction.
Question 3 hints:
Hint 1
You can start by using a calculator to test different heights and get a feel for the relationship.
Hint 2
You need to arrive at an equation in the form d = f(h). Where d is the horizontal distance from the end of the ramp to the landing pad, and h is the height of the ramp.
Step-by-step solutions [for v = 3 m/s]:
Question 1
The answer will depend on the available resources. From timing sensors to video analysis, all answers are valid as long as the measurements are consistent and repeatable.
Question 2
This a projectile motion problem. We can decompose the movement into its x (horizontal) and y (vertical) components.
We want to know the distance traveled horizontally (x), which is given by the formula: x(t) = vx * t But we don’t know the time of flight yet. For that, we need to look at the vertical (y-axis) motion. The car will fly until it reaches the ground, that is when the vertical position is: y(t) = 0. We can compute t by solving the quadratic equation: y(t) = (1/2) * a * t2 + vy * t + y(0) Substituting the values we get:
0 = (1/2) * (-g) * t2 + 3 m/s * sin(35º) * t + 20 cm,
where v is the speed at the moment of takeoff, g is the acceleration of gravity (negative since it points downwards). You can use the Quadratic Formula calculator to obtain the result. The car is in the air for 0.44 seconds. With this value, we can now use the first equation to compute the horizontal distance travelled during that time. The car will land 1.1 m from the ramp.
Question 3
To do this, we need to work with unknowns and manipulate equations. We start by writing the equations of motion for the x-axis and the y-axis:
Vertical: 0 = (1/2) * a * t2 + vy * t + h Horizontal: d = vx * t We now have 2 equations and 2 unknowns (t and d, since y(0) = h is considered a parameter), so we start solving by making t the subject of the Horizontal equation: t = d / vx We can substitute the expression in the Vertical equation: 0 = (a * 1/2) * (d / vx)2 + (d * vy) / vx + h Rearranging, it is clear that this is a quadratic equation: [a/(2 * (d / vx2)] * d2 + [vy / vx] * d + h = 0 with: a = -g = -9.8 m/s2 vx = v * cos(θ) = 3 m/s * cos(35º) vy = v * sin(θ) = 3 m/s * sin(35º)
Solving for d we obtain the result we were looking for. The solution is:
Dear teacher! We're in an early stage of this project. Our main objective right now is to learn how to make scenarios that best suit your needs. Please use the comment box below to tell us:
Is the difficulty level right for your class?
How would you use it in class?
How would you improve this scenario?
A bonus: what are you teaching next week? We'd love to prepare a scenario for you
3 thoughts on “Car Jump (Advanced)”
Everything is very open with a precise description of the
issues. It was definitely informative. Your website
is useful. Thank you for sharing!
Thank you so much! I’m glad you found it useful
I’m really curious, how would you use this scenario in class?
Maybe we could create a scenario especially for your students
Everything is very open with a precise description of the
issues. It was definitely informative. Your website
is useful. Thank you for sharing!
Thank you so much! I’m glad you found it useful
I’m really curious, how would you use this scenario in class?
Maybe we could create a scenario especially for your students