This scenario tests basic arithmetic, unit conversion, and time calculations.
Recommended grade: 6th.
Difficulty level: Basic.
This scenario was originally created by Kamil Wesołowski, Kacper Pogwizd, and Jakub Wojnar-Płeszka, students at the Cracow University of Economics.
Scenario:
Sylvia and Michael own a pizza place, “Omni Hut“, on a small island that’s a part of a big archipelago. One of the other islands is home to their good friend Frankie the Bear, who’s developed quite a taste for their product.

- Frankie is having some family over for dinner, so he decided to order 27 square feet of pizza. “Omni Hut” offers pizzas that are 28 inches in diameter and cost $25. How much will the bear pay for his order?
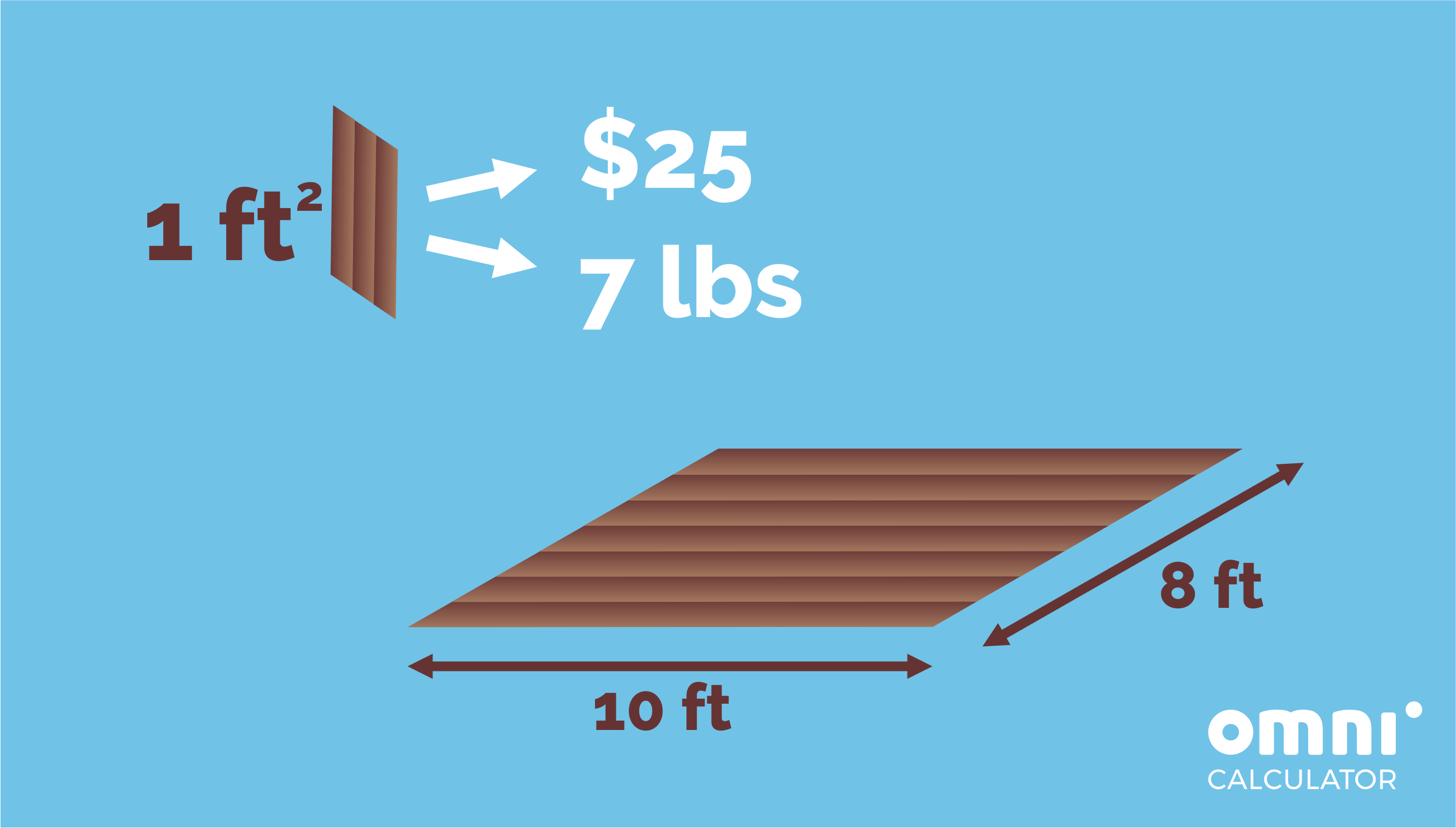
- In order to deliver the pizza, Sylvia and Michael have to build a raft to travel from one island to the other. It should fit both of them comfortably, along with the order. They decided the raft should be rectangular with sides of length 10 and 8 feet. If each square foot of materials costs $1.20 and weighs 7 lbs, how much will the raft cost?

- Only 25% of what “Omni Hut” makes on the deal goes into the pockets of the workers. How much will Sylvia and Michael make on the order? Remember to take into account the cost of transport.
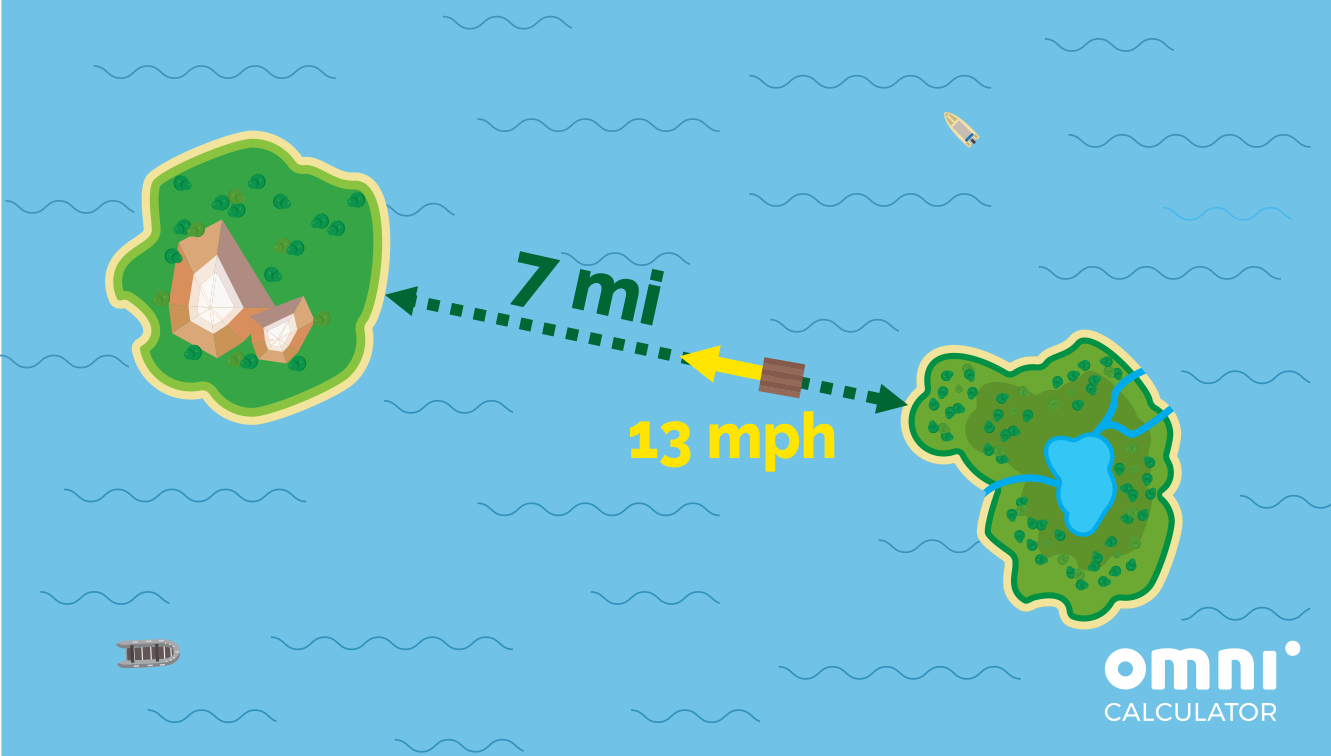
- Frankie’s island is 7 miles away from “Omni Hut“. How much will it take to travel there and back if the raft moves at an average speed of 13 miles per hour? Assume that preparing the pizza takes 1 hr 20 min and packing it takes 10 min. When will they be back if they leave their place at 10 am?
Useful calculators:
- Conversion calculator – https://www.omnicalculator.com/conversion/conversion-calculator
- Pizza size calculator – https://www.omnicalculator.com/food/pizza
- Circle calculator – https://www.omnicalculator.com/math/circle
- Area of a rectangle calculator – https://www.omnicalculator.com/math/rectangle
- Square footage calculator – https://www.omnicalculator.com/math/circle
- Percentage calculator – https://www.omnicalculator.com/math/percentage
- Return on sales calculator – https://www.omnicalculator.com/finance/ros
- Drive time calculator – https://www.omnicalculator.com/everyday-life/drive-time
Question 1 hints:
Question 2 hints:
Question 3 hints:
Question 4 hints:
Solutions:
Step-by-step solution:
r = d / 2 = 28 in / 2 = 14 in.
Now we can use the circle calculator to find the area:
pizza_area = π * r² ≈ 3.14 * (14 in)² ≈ 615 in².
Observe that Frankie would like 27 square feet of pizza, and the above area is expressed in square inches. In order to proceed with the calculations, we need to convert the units so that they agree. The conversion calculator gives
pizza_area ≈ 615 in² ≈ 4.27 ft².
Note that, alternatively, we could have changed the 27 square feet into square inches.
Next, we need to find how many pizzas Frankie should order. To do that, we divide the area he’d like to have by the area of a single pizza:
no_of_pizzas = desired_area / pizza area ≈ 27 ft² / 4.27 ft² ≈ 6.32,
which means that he needs to order 7 pizzas.
Lastly, we multiply the number of pizzas by the cost of one:
total_cost = 7 * $25 = $175.
Warning: Alternatively, we could have used the pizza size calculator and saved ourselves some trouble with unit changes by simply picking the one we want from the list in the calculator. Observe, however, that this would lead to some discrepancy: it would tell us that the area of a single pizza is 4.28 ft² as opposed to the 4.27 given above. This is due to some rounding up along the way. Still, the final answer of 7 pizzas stays the same.
raft_area = a * b = 10 ft * 8 ft = 80 ft².
Now we need to find how much it will cost. Since each square foot of materials costs $1.20, we’ll need
raft_cost = raft_area * $1.20 = 80 * $1.20 = $96.
Note that we haven’t found the total weight of the materials, as the question didn’t ask for it.
income = total_cost – raft_cost = $175 – $96 = $79.
Now it’s time to count how much of that goes to their pockets. We know that only 25% of the amount gets transferred to the workers, so the percentage calculator tells us that it is
profit = 25% * income = 0.25 * $79 = $19.75.
Since the distance between “Omni Hut” and Frankie is dist = 7 mil, the total Sylvia and Michael have to travel is twice that (because they also have to return), which is
total_dist = 2 * dist = 2 * 7 mil = 14 mil.
From the scenario, we know that they are traveling at an average speed of v = 13 mph. Therefore, the drive time calculator tells us that it will take them
time = total_dist / v = 14 mil / 13 mph ≈ 1.08 hr.
Now we’d like to know what time they’ll be back if they leave at 10 am. To make our lives easier, let’s first change the time a little:
time ≈ 1.08 hr = 1.08 * 60 min = 64.8 min ≈ 1 hr 5 min.
Therefore, since
10 hr + 1 hr 5 min = 11 hr 5 min,
they’ll be back around 11:05 am.