3D geometry – An order of mine (basic)

Concepts addressed: square pyramid volume, triangular prism volume, percentages.
Recommended grade: 7th.
Difficulty level: Basic.
An advanced version of An order of mine is also available.

Scenario:

You own a smithy in a small rural town some few miles away from some high mountains. Today seemed like just another lazy day, but suddenly a very short, bearded man enters your shop and greets you with a thick accent you don’t recognize. He sure is an odd client, but he soon attracts your attention with the big order he wants you to make.

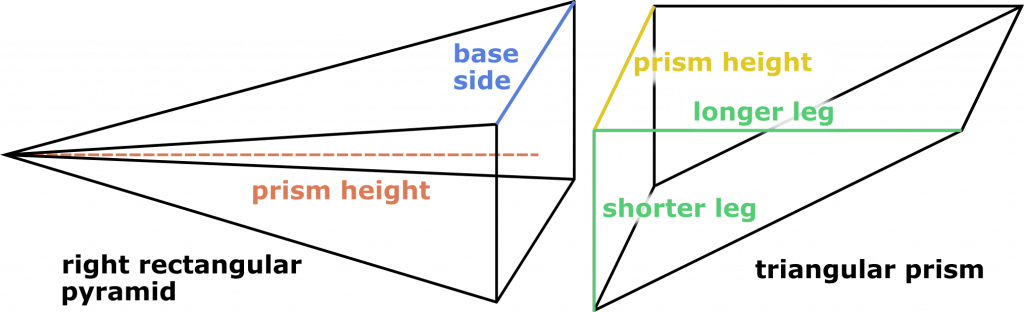
1. The client would like you to prepare for him twenty-five pickaxes. The head of each pickaxe has on one side a right square pyramid, which is 9-inches high, with a 3-inch base edge, and on the other side a triangular prism, which has a height of 3 inches and whose base is a right triangle with legs that are 3- and 6-inches long. What volume of metal do you need to fulfil the order if each pickaxe needs additional three cubic inches of metal for the joint between the two parts?

2. The visitor offers you $9,000 for the whole order. You buy the metal for $5 per cubic inch, and every pickaxe needs a $5 wooden handle. How much are you going to earn on this deal if you have to subtract 15% from the shop’s profit to pay the local girl that helps you?

Useful calculators:

• Right rectangular pyramid calculator – https://www.omnicalculator.com/math/right-rectangular-pyramid
• Triangular prism calculator – https://www.omnicalculator.com/math/triangular-prism
• Percentage calculator – https://www.omnicalculator.com/math/percentage

Question 1 hints:

Question 2 hints:

Solutions:

Step-by-step solution:

Question 1

Let’s begin by calculating the volume of metal we need for a single pickaxe. The scenario tells us that its head has two parts: a right square pyramid, and a right triangle prism. The first one has a height, h_pyramid, of 9 in, and a base side, a, of 3 in. Therefore, the right rectangular pyramid calculator gives that its volume is
V_pyramid = (a² * h_pyramid) / 3 = ((3 in)² * 9 in) / 3 = 27 in³.

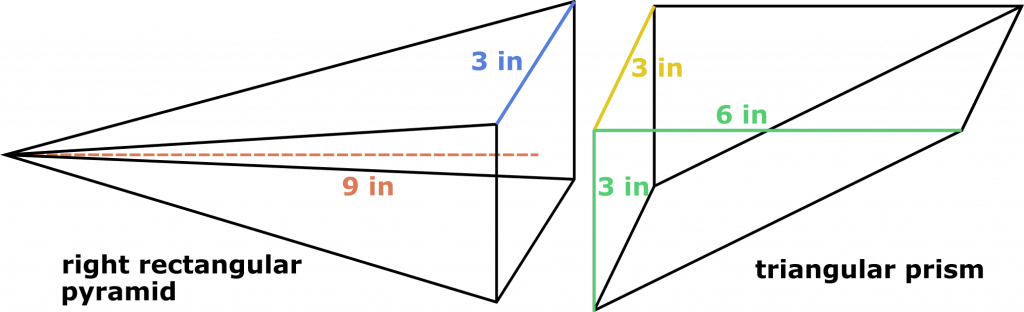
On the other hand, the prism has a right triangular base, with legs b = 3 in and c = 6 in. Observe that we can easily calculate the area of this triangle since b can be its height, and c its width (or vice versa). Moreover, the prism has a height, h_prism, of 3 in. Now we use the triangular prism calculator to get
V_prism = h_prism * (b * c) / 2 = 3 in * (3 in * 6 in) / 2 = 27 in³.

We are now ready to calculate how much metal is needed for a single pickaxe. Remember that each requires an additional 3 in³ for the joint. This means that:
V_pickaxe = V_pyramid + V_prism + 3 in³ = 27in³ + 27 in³ + 3 in³ = 57 in³.

Lastly, we multiply the volume needed for one pickaxe by the number the client ordered:
V = 25 * V_pickaxe = 25 * 57 in³ = 1,425 in³.