Concepts addressed: cylinder volume, cone volume.
Recommended grade: 9th
Difficulty level: Basic.
An advanced version of Hair volume is also available.

Scenario:
Every shampoo advert tell us that their product will boost our hair’s volume, but have you ever wondered what the volume of our head of hair actually is? We know, right, who hasn’t?! The average hair is about 0.003 in thick. The average human head has about 100,000 hair follicles.
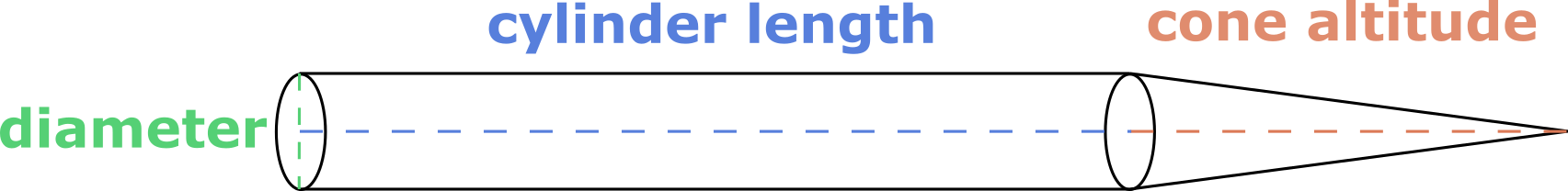
- On average, a human hair grow about 0.5 inches every month. How much additional volume will a person grow in half a year, if they started off bald? For simplicity, let’s say that two-thirds of a hair’s length is a cylinder, while the remaining length is a right circular cone (see the diagram below).
- A man’s facial hairs tend to be thicker than their head hairs. If we assume that the average beard hair is 0.004 in thick and the average beard consists of 30,000 such hairs, what takes up more volume: Gandalf’s stylish 6-inch-long hairdo or his magnificent 9-inch-long wizardly beard?
Useful calculators:
- Cylinder volume calculator – https://www.omnicalculator.com/math/cylinder-volume
- Right circular cone calculator – https://www.omnicalculator.com/math/right-circular-cone
- Conversion calculator – https://www.omnicalculator.com/conversion/conversion-calculator
Question 1 hints:
Question 2 hints:
Solutions:
Step-by-step solution:
The description tells us that one part of it is a cylinder, and the other part is a cone. Also, the cone makes up a third of the length of a hair, and we want the hair to be 3-inch-long, so the cone’s height will be h_cone = 3 in / 3 = 1 in. This means that the cylinder’s height will be h_cylinder = 2 in. Moreover, a hair is 0.003 in thick, so this will be the diameter of the base of both the cylinder and the cone. Therefore, the radius of each of them will be half of that, which is r = 0.0015 in.

Now we’re ready to calculate the volumes. Let’s start with the cylinder, using the cylinder volume calculator:
cylinder = h_cylinder * π * r² = 2 in * π * (0.0015 in)² ≈ 0.0000141 in³,
Next is the cone and the right circular cone calculator:
cone = (h_cone * π * r²) / 3 = (1 in * π * (0.0015 in)²) / 3 ≈ 0.0000024 in³.
This means that the volume of a single strand of hair is
strand = cylinder + cone ≈ 0.0000165 in³.
The last thing to do is to calculate the volume of all 100,000 hairs:
V = 100,000 * strand ≈ 1.65 in³
We’ll begin with the head hair. Again, we divide it into a cylinder and a cone, where the cylinder’s height, h_Hcylinder, is 4 in (two-thirds of the whole 6 inches of length), and the cone’s height, h_Hcone, is 2 in.

Now we move on to finding the volume of each shape by using the cylinder volume calculator and the right circular cone calculator respectively:
head_cylinder = h_Hcylinder * π * r² = 4 in * π * (0.0015 in)² ≈ 0.0000282 in³,
head_cone = (h_Hcone * π * r²) / 3 = (2 in * π * (0.0015 in)²) / 3 ≈ 0.0000047 in³.
Adding these two results together gives that the volume of a single head hair, which is:
head_strand = head_cylinder + head_cone ≈ 0.0000329 in³.
Lastly, the volume of all 100,000 of Gandalf’s head hair is
head_V = 100,000 * head_strand ≈ 3.29 in³.
NOTE: We could have also observed that a single hair in Question 2 is twice as long as that from Question 1, and therefore the cylinder and the cone parts’ heights are also twice what they were before. This means that the volume of a single hair, and so also of all the head hairs is twice as much as what we obtained in Question 1. Note, however, that this gives a small difference of 0.01 in³ in the final answer because of rounding.
Now we repeat the calculations for the beard hair. Here the length of the hair is 9 in, which means that the cylinder and the cone have heights h_Bcylinder = 6 in and h_Bcone = 3 in respectively. Moreover, the diameter of the base of such a hair changes to 0.004 in, so the radius is now half of that, which is R = 0.002 in.

Let’s get back to the cylinder volume calculator and the right circular cone calculator and compute
beard_cylinder = h_Bcylinder * π * R² = 6 in * π * (0.002 in)² ≈ 0.0000754 in³,
beard_cone = (h_Bcone * π * R²) / 3 = (3 in * π * (0.002 in)²) / 3 ≈ 0.0000126 in³,
and so the volume of a single beard hair is
beard_strand = beard_cylinder + beard_cone ≈ 0.000088 in³.
Lastly, the volume of all 30,000 of Gandalf’s beard hair is
beard_V = 30,000 * beard_strand ≈ 2.64 in³.
In particular, we see that the hairdo has more volume than the beard.