3D geometry – An order of mine (advanced)

3 Comments / Mathematics / By /

Concepts addressed: cube volume, triangular prism volume, square pyramid volume, cylinder volume, percentages.
Recommended grade: 7th.
Difficulty level: Advanced.
A basic version of An order of mine is also available.

Scenario:

You own a smithy in a small rural town some few miles away from some high mountains. Today seemed like just another lazy day, but suddenly a very short, bearded man enters your shop and greets you with a thick accent you don’t recognize. He sure is an odd client, but he soon attracts your attention with the big order he wants you to make.

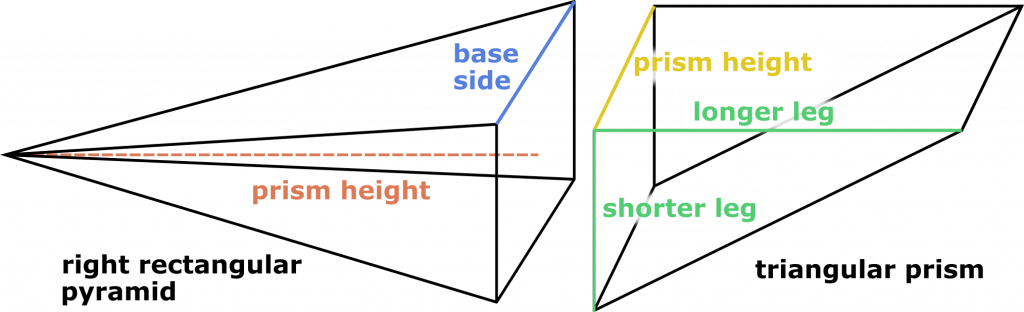
  1. The visitor wants you to prepare for him twenty-five pickaxes. The head of each pickaxe has on one side a right square pyramid, which is 9-inches high, with a 3-inch base edge, and on the other side a triangular prism, which has a height of 3 inches and whose base is a right triangle with legs that are 3- and 6-inches long. What volume of metal do you need to make all of the pyramids and prisms?
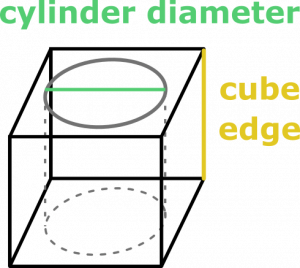
  1. In each pickaxe, the two parts of its head are joined by a joint. It has the form of a cube with a 3-inch-long edge with a hole right through two oposing faces. The hole is in the shape of a cylinder with base diameter of 2.5 in, and is then used to hold the handle. With the joints in mind, how much metal will you need for the whole order?

  1. The visitor offers you a pure gold nugget weighing 6 oz for the whole order. You buy the metal for $5 per cubic inch, and every pickaxe needs a $5 wooden handle. Suppose that gold is worth $1,700 per ounce. How much are you going to earn on this deal if you have to subtract 15% from the shop’s profit to pay the local girl that helps you?

Useful calculators:

Question 1 hints:

Hint 1
Try to sketch what the pickaxe head looks like. What parts does it consist of? Can you describe the sides of the shapes?
Hint 2
What is the volume of the pyramid part? And of the prism part? How many of each do we have to produce?

Question 2 hints:

Hint 1
Try to sketch what the joint looks like. How can we compute the volume of such a shape?
Hint 2
We can look at the joint as a big cube, from which we cut a small cylinder.
Hint 3
If we know the volume of one joint, how much metal will be needed for all twenty-five of them? And how much will be required for all the heads in total?

Question 3 hints:

Hint 1
How much is the gold nugget worth?
Hint 2
From the first question, we know how much metal we need, but how much will it cost us?
Hint 3
What is the cost of all the components needed, i.e., the metal and the handles?
Hint 4
How much did the shop earn on the deal? How can we see how much of that goes to you?

Solutions (WARNING: depends on the current gold value, example for $1,658):

Question 1
V₁ = 1,350 in³
Question 2
V₂ ≈ 1,657 in³
Question 3
earnings ≈ $1,521.50

Step-by-step solution:

Question 1
Let’s begin by calculating the volume of metal we need for a single pickaxe head. The scenario tells us that its head has two parts: a right square pyramid and a right triangle prism. The first one has a height, h_pyramid, of 9 in, and a base side, a, of 3 in. Therefore, the right rectangular pyramid calculator gives its volume as:
V_pyramid = (a² * h_pyramid) / 3 = ((3 in)² * 9 in) / 3 = 27 in³.

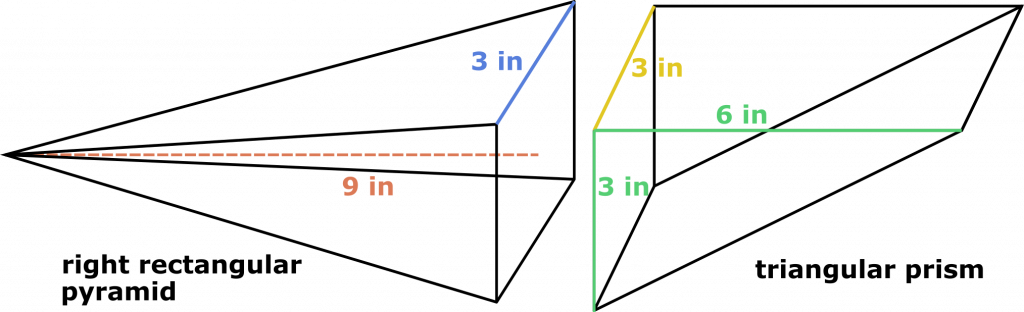
On the other hand, the prism has a right triangular base. We can use the slope calculator to calculate the angle we want: it has legs b & c equal to 3 in and 6 in respectively. Observe that we can easily calculate the area of this triangle since b can be the triangle’s height, and c its width (or vice versa). Moreover, the prism has a height, h_prism, of 3 in. Now we can use the triangular prism calculator to get:
V_prism = h_prism * (b * c) / 2 = 3 in * (3 in * 6 in) / 2 = 27 in³.
Therefore, since we’ll be making 25 pickaxes, we need:
V₁ = 25 * (V_pyramid + V_prism) = 25 * (27 in³ + 27 in³) = 1,350 in³
of metal.

Question 2
To calculate the volume of a single joint, let’s first describe its shape. It is supposed to be a cube with a cylinder hole in it. Therefore, we can calculate the volume of such a shape by subtracting the volume of the cylinder (the hole) from the volume of the cube. Note that the height of the cylinder is equal to the cube’s edge. This gives a = 3 in and h = 3 in. Also, the diameter of the hole is 2.5 in, which means that its radius is half of that, r = 1.25 in.

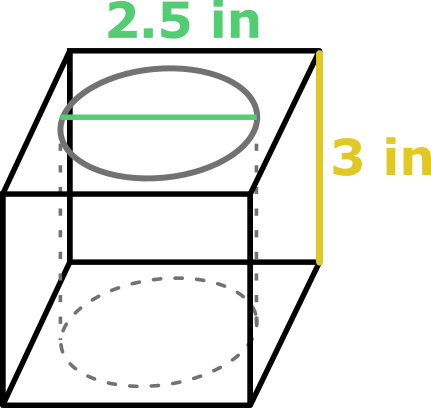
With this we are ready to use the volume of a cylinder calculator:
V_cube = a³ = (3 in)³ = 27 in³,
and:
V_hole = h * π * r² = 3 in * π * (1.25 in)² ≈ 14.72 in³.
Hence, the volume of a single joint is:
V_joint = V_cube – V_hole ≈ 27 in³ – 14.72 in³ = 12.28 in³.

Lastly, we need to calculate how much metal we need for all the pickaxe heads. To do this, let’s take the result of Question 1 and add the 25 joints:
V₂ = V₁ + 25 * V_joint ≈ 1,350 in³ + 25 * 12.28 in³ = 1,657 in³.

Question 3
Let’s begin by calculating the costs of the whole order. We know from Question 2 how much metal we need, so now we can multiply that by the cost of a single cubic inch to obtain:
metal_cost = V₂ * $5 = 1,657 * $5 = $8,285.

Recall that each of the 25 pickaxes needs a $5 handle. This means that:
total_cost = metal_cost + 25 * $5 = $8,285 + $125 = $8,410.

Now let’s calculate the value of the 6-ounce gold nugget. If one ounce of pure gold is worth $1,700, then the shop has received 6 * $1,700 = $10,200 worth of gold. This means that the shop has made $10,200 – $8,410 = $1,790 on this order. Maybe it’s time to reconsider our area of work?

Anyway, the last thing to do is to take away 15% from this sum for the helper. This means that you’ll be left with 100% – 15% = 85% of the profit. The percentage calculator gives that this is:
earnings = 85% * $1,790 ≈ $1,521.50.

Dear teacher! We're in an early stage of this project. Our main objective right now is to learn how to make scenarios that best suit your needs. Please use the comment box below to tell us:
  • Is the difficulty level right for your class?
  • How would you use it in class?
  • How would you improve this scenario?
  • A bonus: what are you teaching next week? We'd love to prepare a scenario for you 🙂

3 thoughts on “3D geometry – An order of mine (advanced)”

  1. This one is new to me. I wonder if the triangular prism would be, more precisely called a right triangular prism? But the sketch, and text that is included makes it perfectly clear.

    In my experience, in the northeastern US, almost all of our work in science classes (perhaps more than 90%) is done in SI units (meters, kilograms, seconds), but a lot of math work is still done in the old British units like inches. My nation seems to be stuck using two systems and it causes problems with our space program at times.

    Reply

  2. Ha, I had to look for the definition of catheti, although I could have guessed. I always called those sides that compose the right angle “legs”, but I like catheti a lot better now.

    Reply

    1. Thank you very much for your kind words! We’ve changed the “cathethi” to legs, just in case there is any confusion. Also, we’ve added a step-by-step solution to all problems. I hope you’ll find it useful to you and your students.

      Reply

Leave a Reply

Your email address will not be published.