Concepts addressed: percentages, unit conversion, quadratic formula, sphere volume.
Recommended grade: 9th.
Difficulty level: Advanced.
A basic version of A plant in your stomach is also available.
Scenario:
Remember how, as a kid, we were told that if we accidentally swallowed a fruit seed, a tree will grow inside our stomachs? It seems funny today, but oh man, we didn’t feel like laughing back then. Fortunately, today we know that such a thing is impossible, but what if it wasn’t?
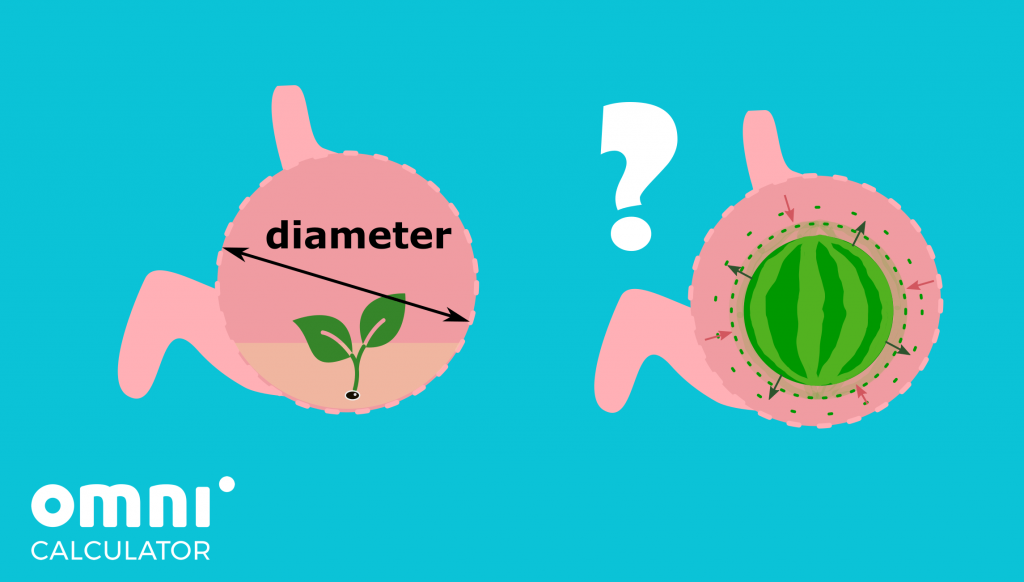
- Let’s say that you’ve swallowed a watermelon seed. Assume for simplicity that your stomach is in the shape of a sphere with a diameter of seven inches, and that all watermelons grow to be spherical. What is the maximum volume a watermelon could reach inside your stomach, if the stomach’s muscles can stretch up to a 10% larger shape, and there’s a quarter gallon of stomach acid already in it?
- Say that a watermelon with a diameter of 4 inches has actually grown in your stomach, and that a cubic inch of watermelon weighs 1.1 ounces. If your stomach digests 12 ounces every day and the watermelon grows in diameter by 0.1 inches a day, will the watermelon keep growing, or will it be slowly digested? For simplicity, assume that you don’t eat anything else while the fruit is inside of you, and that digestion occurs all at once at the end of the day.
- With the same parameters as in the second question, how big would the starting watermelon have to be so that it was in a state of equilibrium, i.e., it grows in a day as much as is digested?
Useful calculators:
- Sphere calculator – https://www.omnicalculator.com/math/sphere
- Percentage calculator – https://www.omnicalculator.com/math/percentage
- Quadratic formula calculator – https://www.omnicalculator.com/math/quadratic-formula
- Conversion calculator – https://www.omnicalculator.com/conversion/conversion-calculator
Question 1 hints:
Question 2 hints:
Question 3 hints:
Solutions:
Step-by-step solution:
stomach = (4 / 3) * π * r³ ≈ 179.5 in³.
We know that muscle stretching increases this volume by 10%. Therefore, it will make the stomach’s volume to be 100% + 10% = 110% of what we calculated above. The percentage calculator gives that this is
stomach_max = 110% * V ≈ 197.5 in³.
It’s time to take the stomach acid into account. Since the conversion calculator says that 0.25 US gal = 57.75 in³, the remaining space for the watermelon to grow is
V = stomach_max – acid ≈ 140 in³.
V_big = (4 / 3) * π * R³ ≈ 36.1 in³,
V_small = (4 / 3) * π * r³ ≈ 33.5 in³.
Therefore, the watermelon grows by
V_big – V_small = 2.6 in³
in a day. Based on the information from the scenario, this extra volume weights 2.6 * 1.1 oz = 2.86 oz. This is clearly less than we digest in a day, meaning that the fruit will slowly be digested.
Let’s start by trying to describe symbolically the volume that our fruit grows. If it’s starting radius is r, and it grows in diameter by 0.1 in a day, then its end radius will be r + 0.05 (remember that diameter is equal to twice the length of the radius). Therefore, according to the formula in the sphere calculator, the starting volume can be described as
V_start = (4 / 3) * π * r³,
and the end volume as
V_end = (4 / 3) * π * (r + 0.05)³.
The volume growth will be equal to the difference between these two values. Moreover, the mass growth will be that times the 1.1 oz the watermelon weights per cubic inch. What we now want is for this mass to be equal to 12 oz. In other words, symbolically, we want to have
1.1 * (V_end – V_start) = 12,
or, substituting the two formulas from above,
1.1 * ((4 / 3) * π * (r + 0.05)³ – (4 / 3) * π * r³) = 12.
Observe that we’ve obtained an equation. All we now have to do is to solve it. Let’s begin by dividing both sides by 1.1. This gives approximately
(4 / 3) * π * (r + 0.05)³ – (4 / 3) * π * r³ = 10.91.
We continue by dividing both sides by 4/3:
π * (r + 0.05)³ – π * r³ = 8.18,
and now similarly by π
(r + 0.05)³ – r³ = 8.18 / π.
We expand the third power of the expression in the brackets:
r³ + 0.15r² + 0.0075r + 0.000125 – r³ = 8.18 / π.
We see that r³ vanishes. This, together with substituting π ≈ 3.14, leaves us with
0.15r² + 0.0075r + 0.000125 = 8.18 / 3.14,
which is a quadratic equation. Now if we move the number on the right side to the left and approximate, we’ll obtain an equivalent equation
0.15r² + 0.0075r – 2.61 = 0.
Using the discriminant formula and the quadratic formula calculator, we calculate its solutions: one is negative (hence not possible), and the other is r ≈ 4.15 in. This means that our starting watermelon would need to be of radius approximately 4.15 in for it to be in the state of equilibrium. Such watermelon would not, however, fit in the stomach.