How fast does a light bulb turn on?

Leave a Comment / Physics / By /

Concepts addressed: velocity in an electric field, electrical power, and analytical skills.
Grade level: 11th

Scenario:

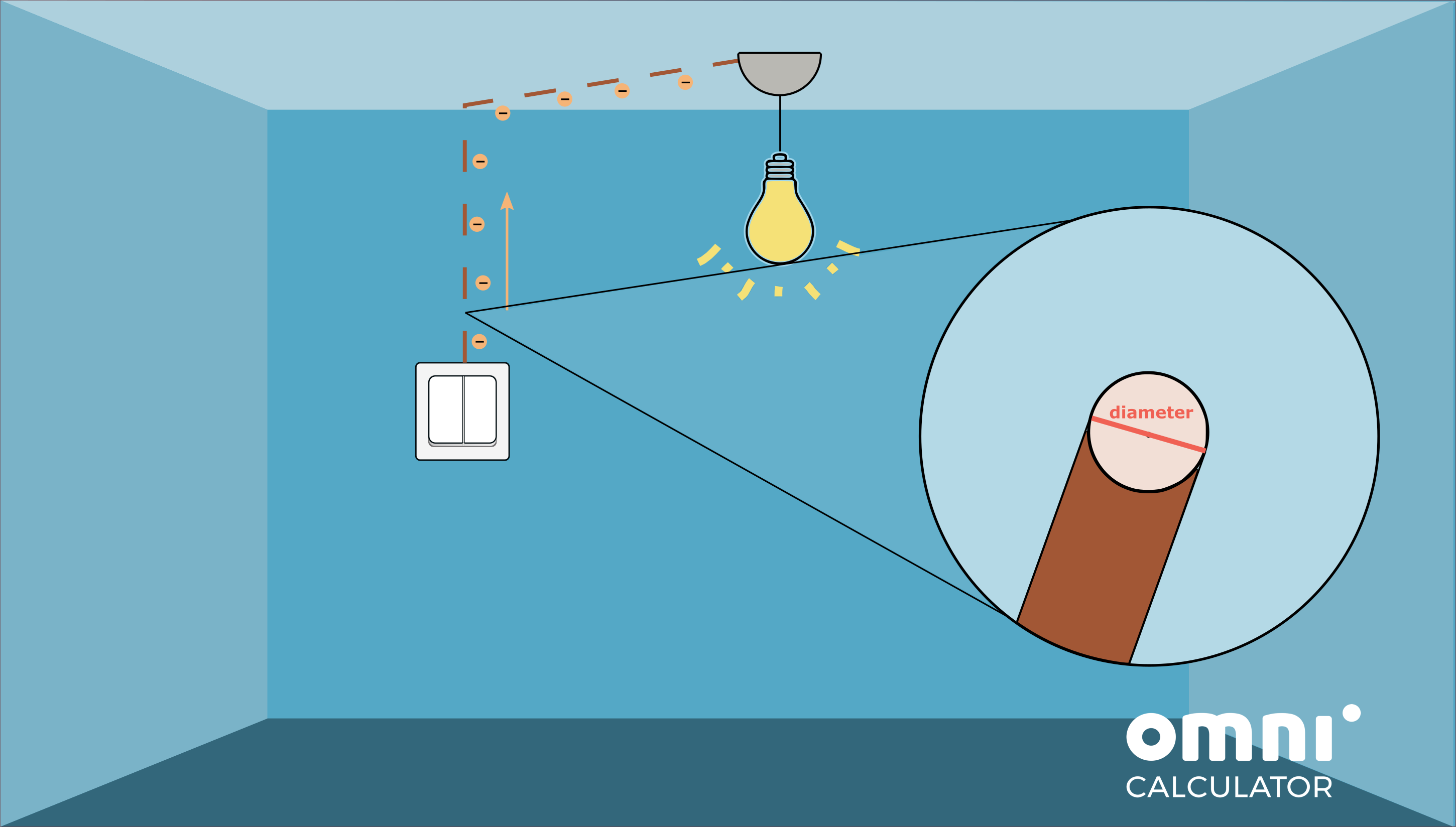
When a light switch is off, the electric circuit inside the wall of your house is interrupted, so neither an electric field nor electrons can flow through it. The moment you flip the switch on you close the circuit, meaning that electrons (and the electric field) are free to flow through the circuit again, and reach whatever device you wanted to power.


Assuming the wiring in your house is full copper 12AWG, and that the length of the cable connecting the switch to the overhead light bulb (60W LED) is 3m.

  1. How long would it take an electron in the switch to reach the light bulb?
  2. Is the result surprising? Why?
  3. Can you explain it? How long would it take light to travel the same distance?

Data:

Diameter of 12 AWG wire: 2.053mm
Voltage of household’s electric system: 220V (EU) || 120V (US)
Density of Carriers in copper: 8.5 1028 carriers/m³
Speed of light: 299 792 458 m/s

Useful calculators:

Question 1 hints:

Hint 1
You need the current going throught the wire to calculate the drift velocity.
Hint 2
You can obtain the current using your home voltage value and the power of the bulb.
Hint 3
speed = distance / time
Solve for time.

Question 2 hints:

Hint 1
Before you calculated anything what did you expect? Hours? Seconds? Miliseconds?
Hint 2
How long does it take the light to turn on after pressing the switch?

Question 3 hints:

Hint 1
Light is an electromagnetic wave.
Hint 2
Changes in electric fields propagate at the speed of light.
Hint 3
A conductor like copper has free electrons everywhere.

Solutions :

Question 1
It takes the electrons 75.1 hours to travel 3m of cable.
Question 2
Yes.
Because the light turns on immediately
Question 3
The electric field is transmitted at the speed of light and it takes light 0.00000001000692 seconds to travel 3m

Step-by-Step solutions :

Question 1
For an electron, the drift velocity equation is: u = I / (n * A * e) where u is the drift velocity, e is the electron charge, I is the electrical current, A is the cross section area of the cable and n is the density of free electrons in the cable (copper).
The value of n is given, and A can be calculated using A = π r2, or by using the Circumference calculator. We find that A = 13.24mm2.
To calculate I, we can use the power draw formula: P = IV. For a standard American household, V = 120V, and our bulb is 60W, so we get I = 0.5A.
Plugging this data into the Drift Velocity calculator gives a speed of 0.000002773m/s.
All we need to do is use that speed and the length of the cable (distance travelled) to calculate time using V = d/t. You can do it by hand or with a calculator, and you will see that it takes the electrons 75.1 hours to travel along 3m of cable.
Question 2
Yes it is surprising.
Because it takes hours for an electron to travel the length of the cable, yet the light turns on almost instantly.
Question 3
Electromagnetic fields propagate at the speed of light, so the field reaches the light bulb almost instantly (0.00000001000692 seconds). The copper cable is full of free electrons, so there are some electrons so close to the light bulb that it takes them almost no time to reach it once the electric field gets there.

Dear teacher! We're in an early stage of this project. Our main objective right now is to learn how to make scenarios that best suit your needs. Please use the comment box below to tell us:
  • Is the difficulty level right for your class?
  • How would you use it in class?
  • How would you improve this scenario?
  • A bonus: what are you teaching next week? We'd love to prepare a scenario for you 🙂

Leave a Reply

Your email address will not be published.