2D geometry – A day at the beach (basic)

Concepts addressed: circle area, circle perimeter, sector of a circle area.
Recommended grade: 10th.
Difficulty level: Basic.

Scenario:

It’s a sunny summer morning and you’re thinking about going to the beach for a few hours. Actually, why not take your witty little sister with you, she could use some exercise with all the candy bars she’s been eating this year.
When you arrive and settle down, she immediately rushes to play in the water. You’re not that good a swimmer, so you get a little worried. Fortunately, you see that there’s a few lifeguards along the shore.

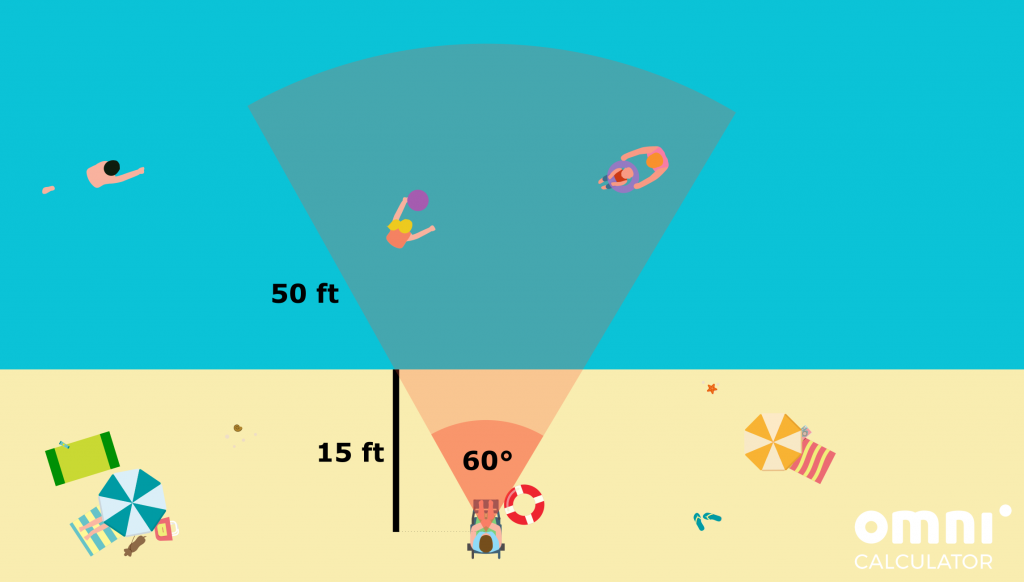
1. Every lifeguard tower is fifteen feet away from the ocean, and the person sitting there keeps their eye on a 60-degree-wide sector straight in front of them. Assume that they can see up to a maximum of 50 feet away from the tower. How big is the area of water in which you can safely let your sister play, so that she is always in the view of one particular lifeguard? For simplicity we suppose that they look straight ahead and don’t move their heads at all.

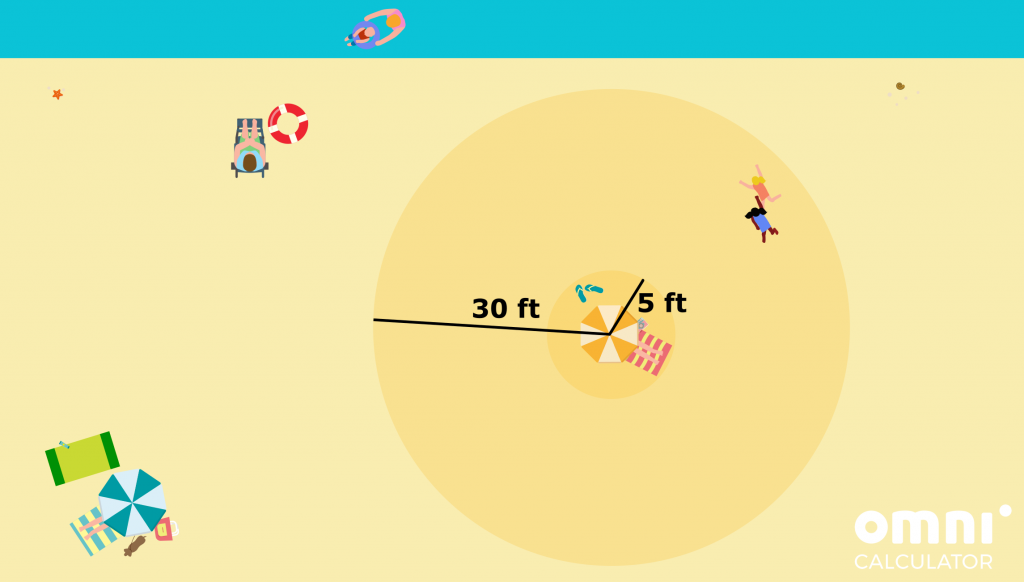
2. After some time in the water your sister comes back to you with a friend she’s just made. They decide to play tag and start running around wildly . You tell your little sister not to run farther than 30 feet away from where you’re sitting so she doesn’t get lost. Also, you tell them to play at least 5 feet away from you, so that they don’t kick up sand onto the towels. What is the area of their play zone you have just established?

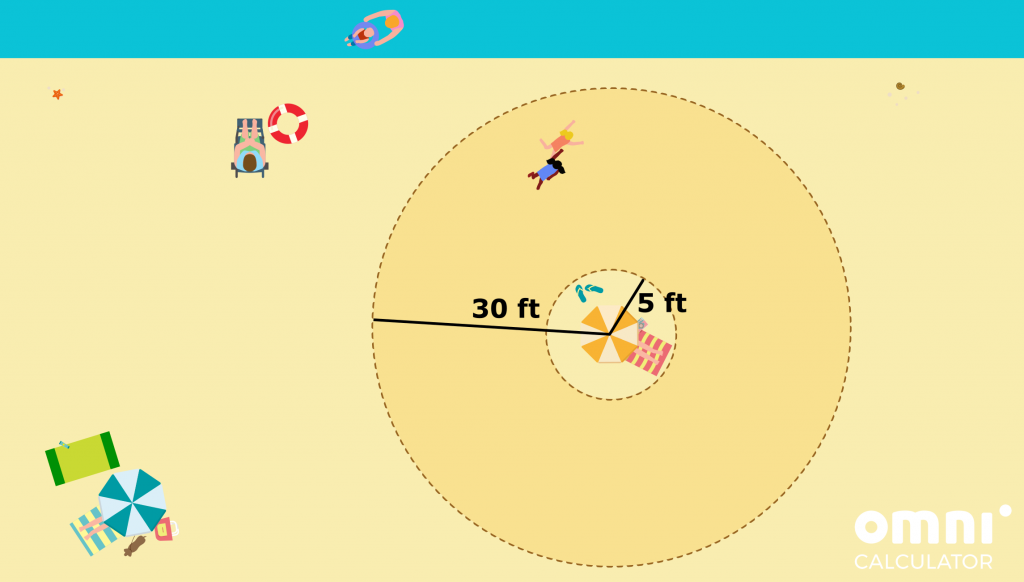
3. You were hoping that your sister and her friend would soon get tired and sit down, but apparently they have much more energy in them than you thought. Remember when we used to have that much energy? Yeah, we don’t either. Anyway, they keep trespassing both sides of the perimeter you’ve established, so you decide to mark it with a few sticks and stones. What is the perimeter of the zone?

Useful calculators:

• Sector area calculator – https://www.omnicalculator.com/math/sector-area
• Arc length calculator – https://www.omnicalculator.com/math/arc-length
• Equilateral triangle calculator – https://www.omnicalculator.com/math/equilateral-triangle
• Circumference calculator – https://www.omnicalculator.com/math/circumference
• Circle calculator – https://www.omnicalculator.com/math/circle

Question 1 hints:

Question 2 hints:

Question 3 hints:

Solutions:

Step-by-step solution:

Question 1

Let’s try to describe the shape in question. The lifeguard can see as far as 50 ft away from their post, but only in a 60-degree angle in front of them. Therefore, the area he watches is a part of a circle. To be precise, it is 1/6th of a circle, as a whole circle is 360 degrees, and 60/360 = 1/6. The circle’s radius, r, is 50 ft.

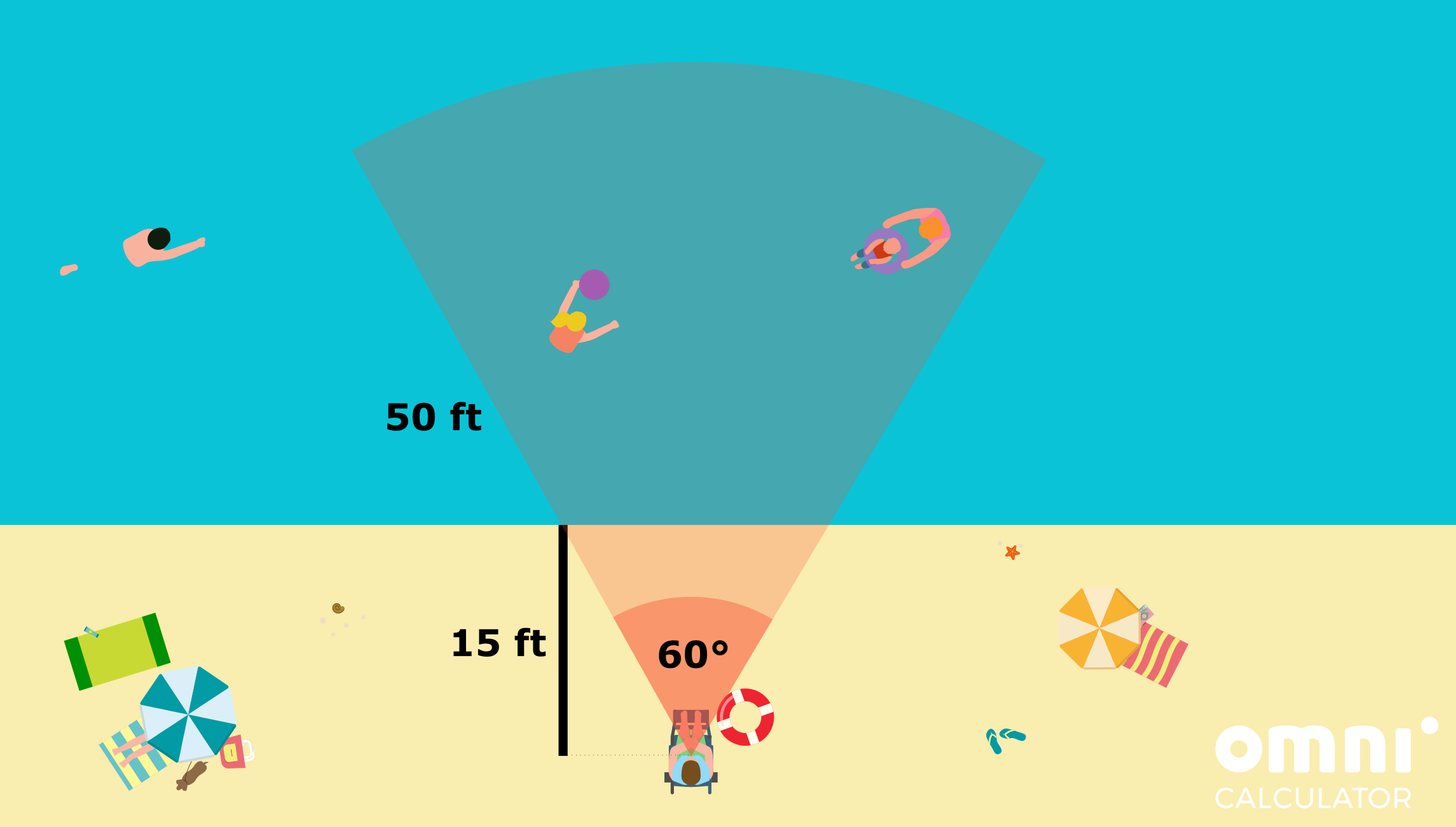
If we now use the formula for the area of a sector of a circle, or simply the sector area calculator, we’ll get that the lifeguard watches approximately
sector = 1/6 * π * r² = 1/6 * π * (50 ft)² ≈ 1308 ft².

However, not all of this is water – the lifeguard can also see a bit of the beach. We can easily see that this sandy section is a triangle. But there is more! Since the line of the sea is perpendicular to the lifeguard’s line of sight, and the angle is 60 degrees, it is, in fact, an equilateral triangle.

The scenario says that the water is 15 ft away from the lifeguard, so the height of the triangle, h, is just that – 15 ft. If we denote the side of the triangle with a, we can use the relationship between the height and the side which is described by the formula:
h = (a * √3) / 2.
Plugging in our numbers gives:
a = 2 * h / √3 = 2 * 15 ft / √3 ≈ 17.3 ft.
This, in turn, allows us to calculate the area of the triangle with the equilateral triangle calculator:
triangle = a * h / 2 = (17.3 ft * 15 ft) / 2 ≈ 129 ft².

The last thing to do is subtract the area of the triangle from the area of the circular sector to obtain the final answer:
A = sector – triangle ≈ 1308 ft² – 129 ft² = 1179 ft²

Question 2

Observe that by saying that the girl shouldn’t run farther than 30 ft away from you, you want her to stay in an area given by a circle of radius R = 30 ft, with you at its origin. Similarly, you wish her not to run into the circle of radius r = 5 ft, with you again at its origin. This means that the area we’re looking for is simply the area between the two circles.

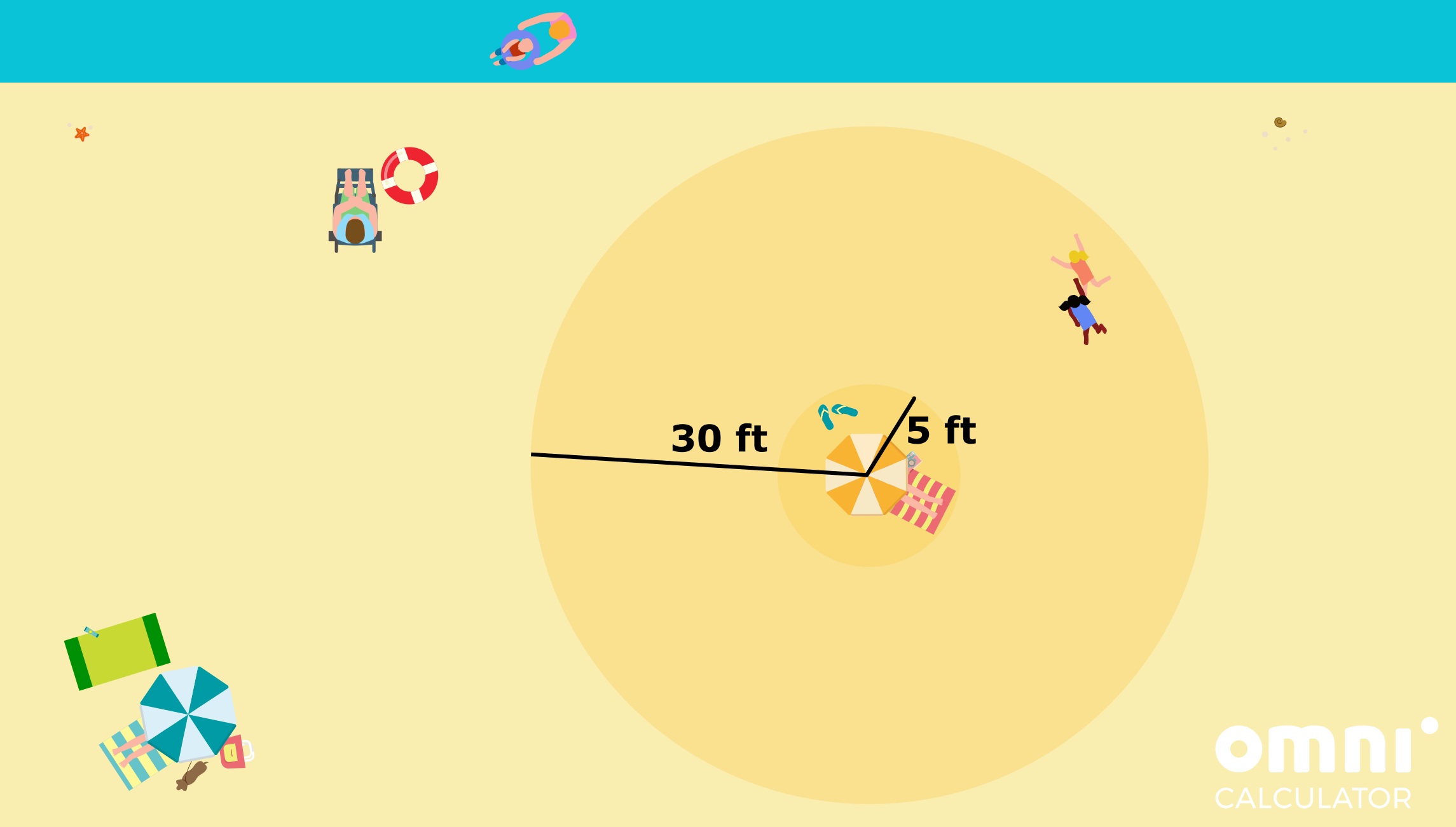
We calculate it by calculating both of the areas with the circle calculator, and then by subtracting the smaller one from the larger circle:
A = π * R² – π * r² = π * (30 ft)² – π * (5 ft)² ≈ 2749 ft².

Question 3

Recall the shape we had in the second question. The shape in this question is exactly the same. We just want to calculate its perimeter, rather than its area.

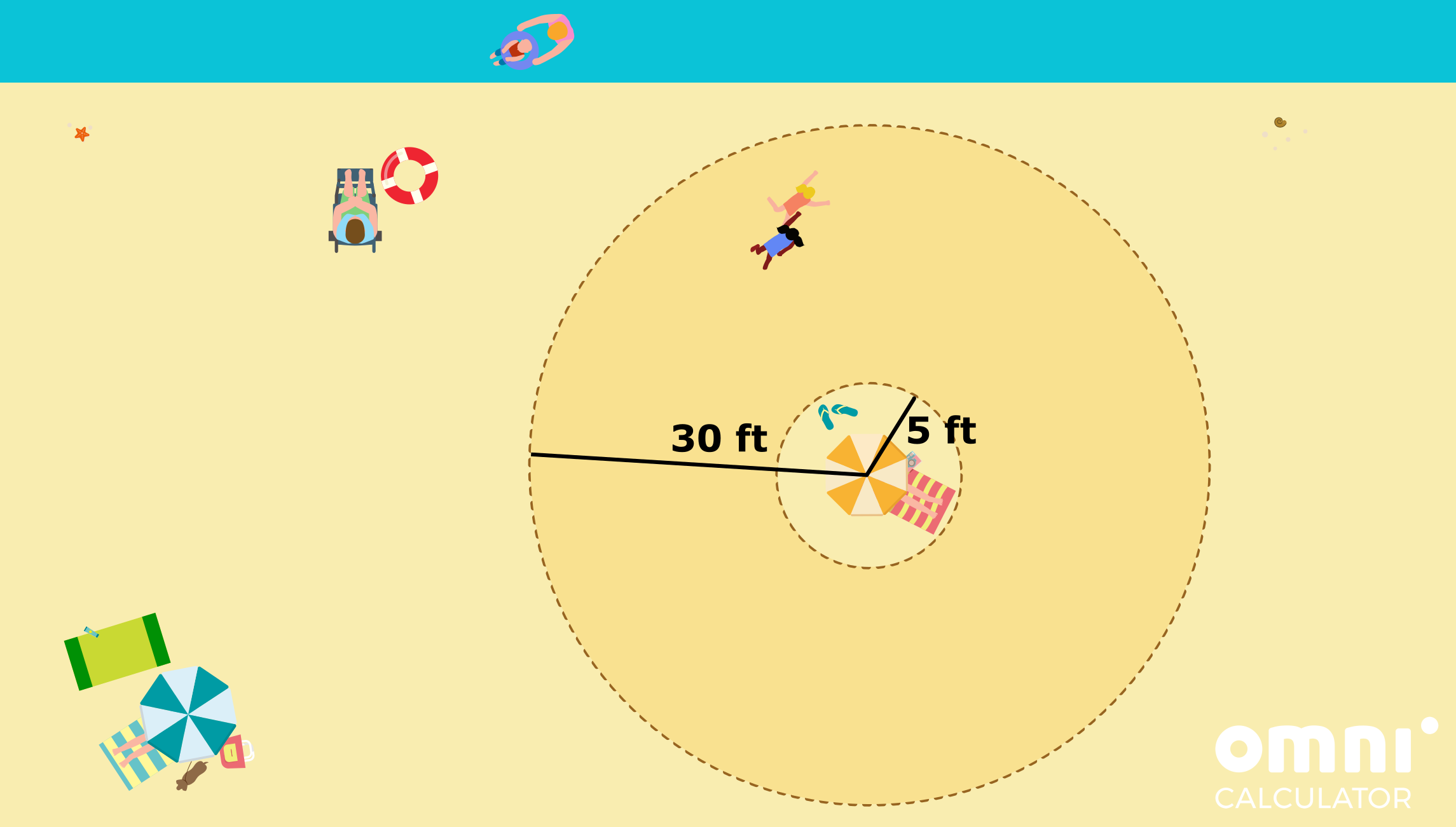
Since the perimeter consists of the bigger circle of radius R = 30 ft and the smaller one of radius r = 5 ft, the circumference calculator gives
perimeter = 2 * π * R + 2 * π * r = 2 * π * 30 ft + 2 * π * 5 ft ≈ 220 ft.