Concepts addressed: rectangle area, rectangle perimeter, square perimeter.
Recommended grade: 5th.
Difficulty level: Basic.
An advanced version of Helping out on the ranch is also available.
Scenario:
Good Ol’ Uncle Joe invited you to his ranch for the weekend to help him set up an enclosure for his horses. He has 50 horses, and they should each have at least 25 square feet of land to be comfortable.
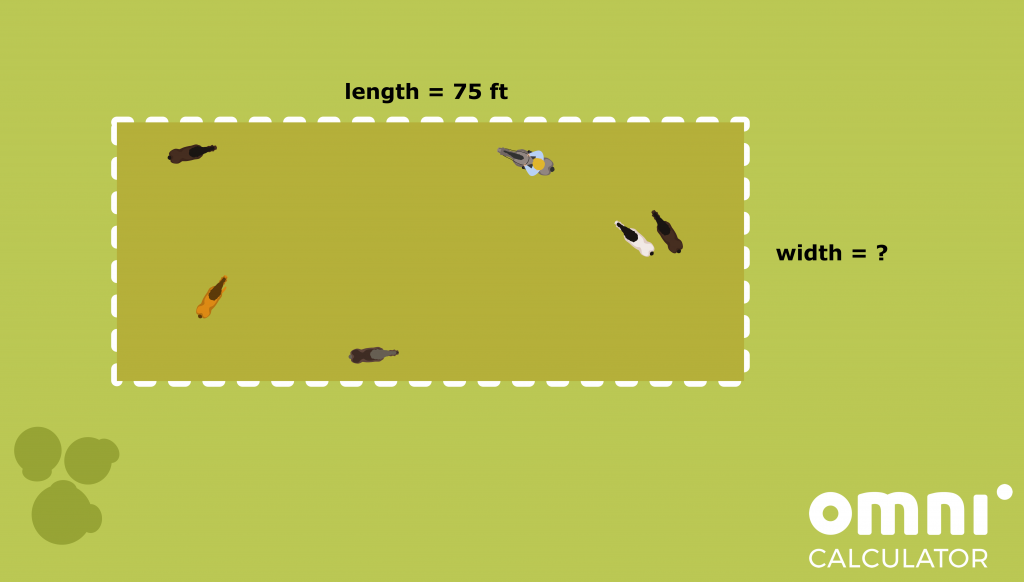
- Uncle Joe wants a rectangular enclosure, and has decided the enclosure should be 75 feet long. How wide should it be?
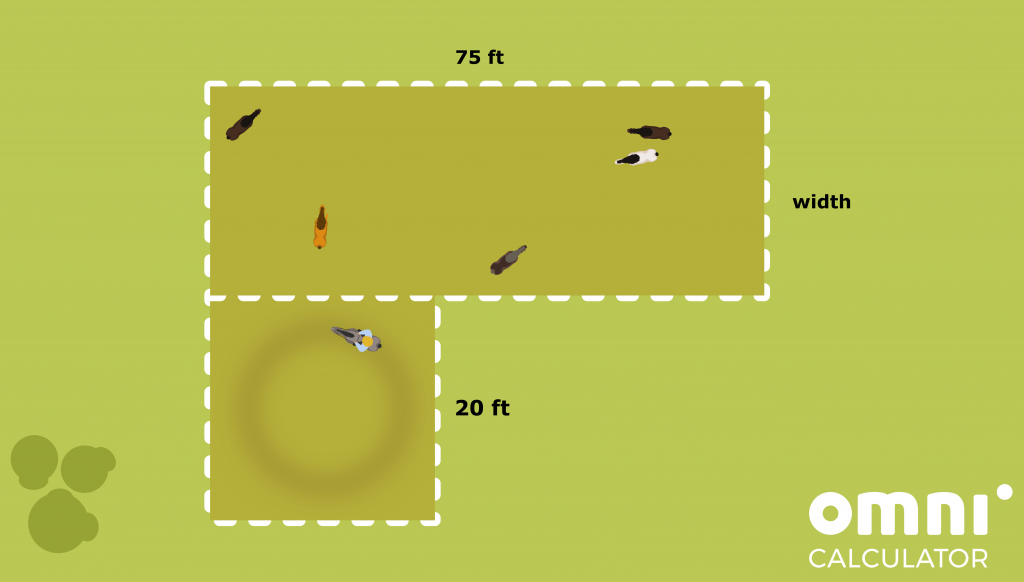
- You decide to add a 20-foot-long square to the outside of the pasture, adjoining its longer side, in case you have to separate a few of the animals. How many feet of fencing do you have to buy to build both enclosures? Remember that the big and the small pastures are separated from each other by a single fence.
Useful calculators:
- Area of a rectangle calculator – https://www.omnicalculator.com/math/rectangle
- Area of a square calculator – https://www.omnicalculator.com/math/square-area
- Perimeter of a rectangle calculator – https://www.omnicalculator.com/math/perimeter-of-rectangle
- Perimeter of a square calculator – https://www.omnicalculator.com/math/square-perimeter
Question 1 hints:
Question 2 hints:
Solutions:
Step-by-step solution:
Now let’s see what we can say about the enclosure we want to set up. According to the scenario, we want it to be rectangular, and we know one of its sides – length = 75 ft. Then using the formula for the area of a rectangle, we need to have
length * width = 1250 ft².
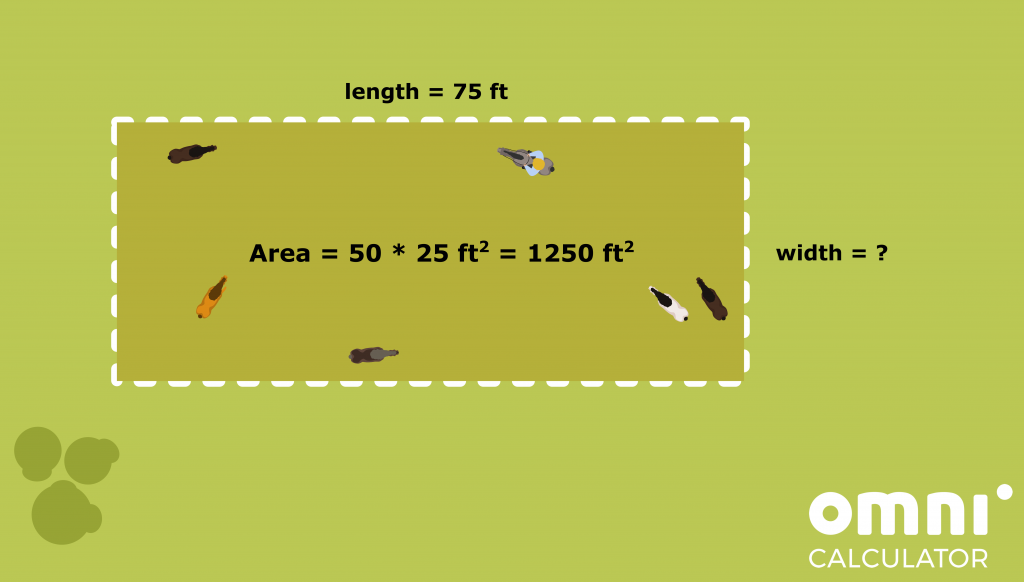
If we put the length the uncle set, we get
75 ft * width = 1250 ft².
With the help of the area of a rectangle calculator, this gives that width = 16 2/3 ft.
rectangle_fencing = 2 * length + 2 * width = 2 * 75 ft + 2 * 16 2/3 ft = 183 1/3 ft.
Now we move on to the additional square enclosure. We want it to have a side of a = 20 ft. But remember that it will adjoin the big rectangular enclosure.
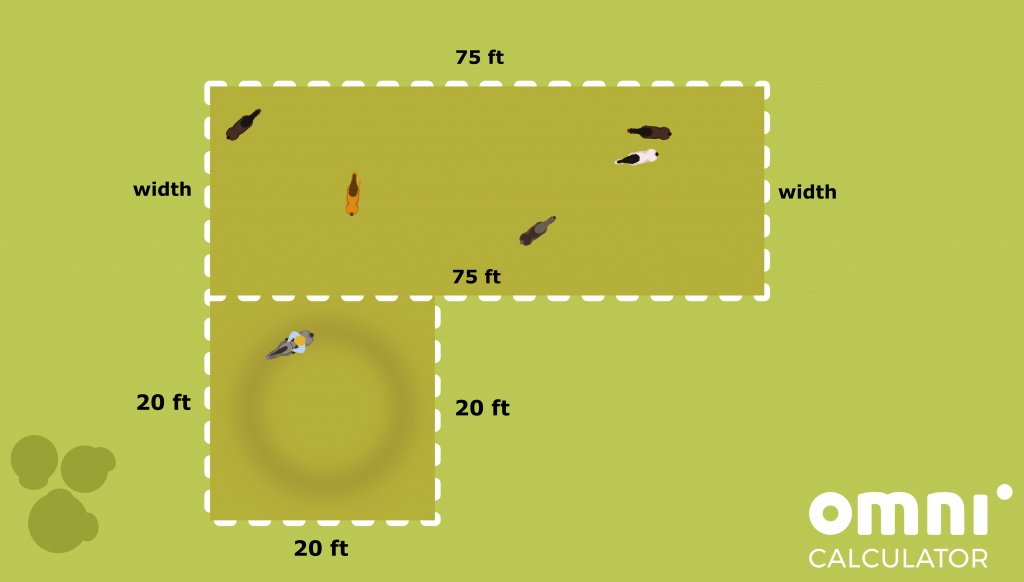
This means that one of its sides will be a part of the fencing of the bigger one. We’ve already counted how many feet of fencing we need for the large one, so it is now enough to take care of only three of the square sides (the fourth is already counted above as part of the bigger enclosure). In other words,
square_fencing = 3 * a = 3 * 20 ft = 60 ft.
Lastly, we must sum the two numbers we obtained to get the total length of fencing we need:
fencing = rectangle_fencing + square_fencing = 183 1/3 ft + 60 ft = 243 1/3 ft.
NOTE: There is a different way of calculating the fencing we need for the square enclosure. If we forget for a second about the rectangular one and focus on the square only, then to put a fence around that one, we will need to put fencing all around it. The perimeter of a square calculator tells us it would be
square_perimeter = 4 * a = 4 * 20 ft = 80 ft.
And now is the time to recall that the two enclosures will be joined together. In other words, they will share a small part of the fence. But we’ve counted the fencing for the rectangular one and the square one separately, so we’ve counted the section that they share twice. However, as the scenario tells us, we want them to be separated by a single fence. This means that when we count all the fencing we need, we have to add the two numbers above, but also subtract from that sum one side of the square, the one that was counted twice. This gives
fencing = rectangle_fencing + square_perimeter – a = 183 1/3 ft + 80 ft – 20 ft = 243 1/3 ft.