Concepts addressed: rectangle area, rectangle perimeter, rectangular prism sketching, percentages.
Recommended grade: 5th.
Difficulty level: Advanced.
A basic version of Helping out on the ranch is also available.
Scenario:
Good Ol’ Uncle Joe invited you to his ranch for the weekend to help him plan out a barn for his horses. He has 14 horses, and each should have a stall of their own, which should be eight feet long and six feet wide.

- If the barn is to have seven stalls on each side and a path that is ten feet wide down the middle, how wide and how long should it be? The stalls should be facing the path with their narrow side.
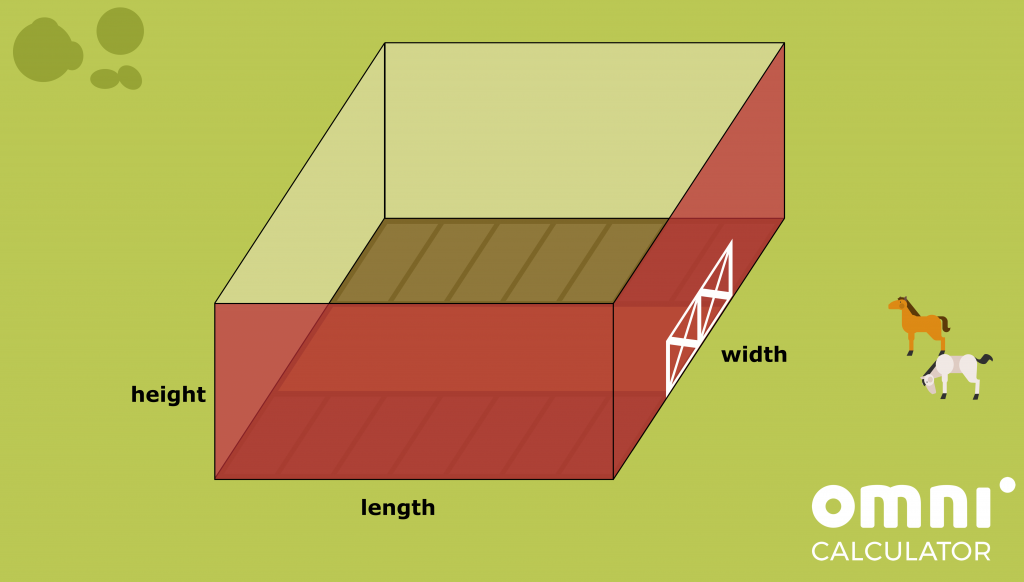
- When it finally gets built, its outside walls will surely need to be painted a nice shade of red. The barn is supposed to be fifteen feet high, and one gallon of paint can cover 400 square feet. How much will the painting cost if a half-gallon can costs $10? Better buy 10% more, just in case some big-town nephew spills some.
Useful calculators:
- Area of a rectangle calculator – https://www.omnicalculator.com/math/rectangle
- Perimeter of a rectangle calculator – https://www.omnicalculator.com/math/perimeter-of-rectangle
- Percentage calculator – https://www.omnicalculator.com/math/percentage
Question 1 hints:
Question 2 hints:
Solutions:
Step-by-step solution:
length = 7 * stall_width = 7 * 6 ft = 42 ft.

To compute the width of the barn, we have to see what are its parts. On one side we have the stalls, in the middle we have the path, and to the right again we have stalls. The stalls are faced with their narrow side (their width) towards the path. This means that they contribute their longer side to the barn’s width. This, together with the 10-foot-wide path, gives
width = stall_length + 10 ft + stall_length = 8 ft + 10 ft + 8 ft = 26 ft.
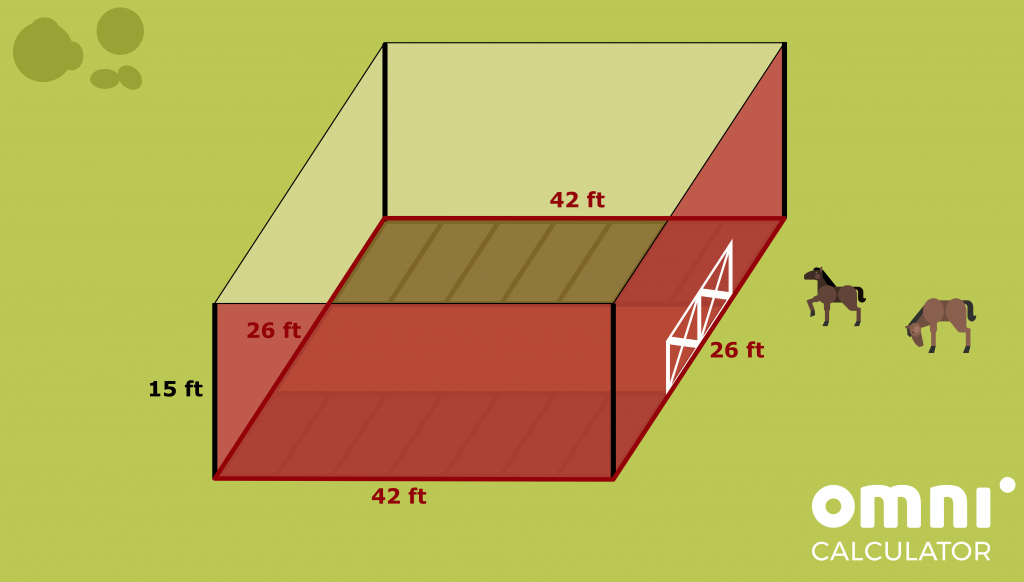
The area of a rectangle calculator comes to help us and gives
area = 2 * h * width + 2 * h * length = 2 * 15 ft * 26 ft + 2 * 15 ft * 42 ft = 2,040 ft².
NOTE: There is a different way of calculating the area we need to paint. We still need to calculate the area of all the walls of the barn, but why not do all four of them at once? To do this, we first observe that all of them have the same height h = 15 ft. Therefore, each side of the rectangle that is the base of the barn (as drawn in question 1) has to be multiplied by the height h to return the area of the wall. So to calculate the total area of all the four walls, we can start by using the perimeter of a rectangle calculator to obtain the barn perimeter:
perimeter = 2 * width + 2 * length = 2 * 26 ft + 2 * 42 ft = 136 ft.
And now we finish by multiplying this by the height h:
area = perimeter * h = 136 ft * 15 ft = 2,040 ft².
Now we move on to the paint. The scenario suggests that every gallon can cover 400 square feet. Therefore, we will need
area / 400 = 2,040 / 400 = 5.1 US gal
of paint to do the whole barn. However, we need to add the extra paint for the potential spillage accidents. The scenario tells us that we should add 10% of what we got above. This means that we need 100% + 10% = 110% of that number. The percentage calculator gives that this is
110% * 5.1 US gal = 5.61 US gal.
Since we’re buying paint in half-gallon cans, in total we’ll need
5.61 / 0.5 = 11.22
cans. Clearly, we can’t buy 0.22 of a can, so in the end we must buy 12 of them. The scenario tells us that one costs $10, so all of them will cost
cost = 12 * $10 = $120.
This is a really cool problem! I want to try it out with my 6th graders next year. One thought and one question.
Thought: I would probably break the second questions into two parts. One to find how much paint and then one to find out about cost. That creates a potential extension for amount and cost of building supplies. Also, if you added in different colors, I think you could easily bring in ratios and proportional reasoning along with Geometry.
Question: could there be a version that involved triangles or irregular shapes? Could it be applied to social distancing measures for classrooms? That would be a really neat way to have students see how this concept applies to their world, especially if they have never been on a farm.
Thank you very much for your comment! I’m really glad you like the problem and I can’t wait to hear your feedback when you try it out with your students 🙂
I also like your thoughts on the scenario. They are a great sketch for a more advanced version or a brand new problem. I promise to keep them in mind for the future!
And as for the question, we’re still gathering feedback from teachers on what scenarios they would like to see, so I think we can expect new problems with new shapes and concepts pretty soon. Also, we’re currently working on preparing the scenarios in a ready-to-print or ready-to-send versions for distance learning.
I’d love to hear your opinion on some other scenarios if you get a chance to look at them 🙂
Take care!
Maciej