Statistics – A streamer’s road to fame (basic)

What values do we need to construct the box-and-whiskers plot? How can we find them?

We begin by writing our data in increasing order, and we need to find the 1st, 2nd, and 3rd quartile, and the least and greatest value.

The 2nd quartile is the median of our numbers. The 1st and 3rd quartiles are the medians of the first and the second half of numbers when they are put into increasing order.

How much did you make on each of the videos? How do we find the average of that?

What data do we have to find the total of if we want to calculate variance?

How do we calculate the standard deviation? Is it somehow related to variance?

We have to calculate the same things as in Question 2. What is different this time?

When calculating the mean and the variance of the new, larger data set, remember to divide the sums by the updated number of total videos.

We’ve already drawn a box-and-whiskers plot in question 1. How do we find the necessary values this time?

Observe that last time we had six values to work with, and now we have seven. How does that change the calculations?

The 2nd quartile is the median of our numbers. The 1st and 3rd quartiles are the medians of the first and the second half of numbers when they are put into increasing order.

average₁ ≈ $3.33, variance₁ ≈ 2.19, standard_deviation₁ ≈ 1.48

average₂ ≈ $2.62, variance₂ ≈ 2.51, standard_deviation₂ ≈ 1.58

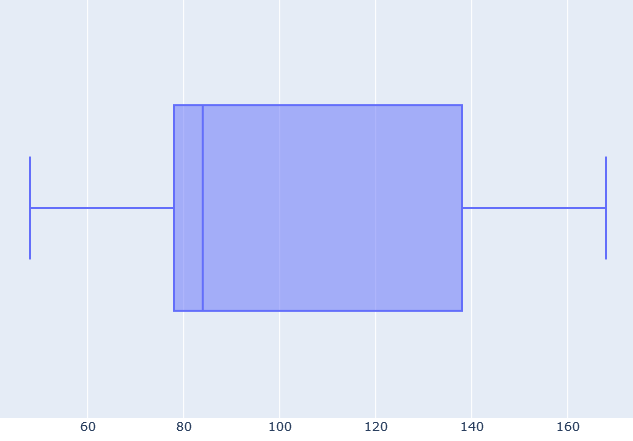
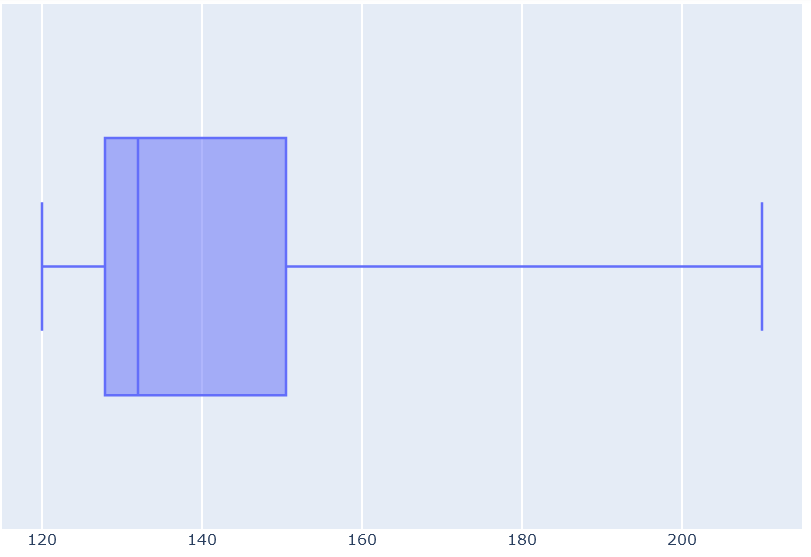
The box this time is much “thinner,” which means that the video lengths are on average of similar lengths. However, the right whisker is quite far from the box. This corresponds to the one very long video, but looking at the whole plot we can deduce that it was more of an exception than a regular thing.

All in all, we can suspect that the famous youtuber’s strategy is to post videos of more or less the same length. To be precise, a bit over 20-minute-long. Also, observe that this differs a lot from the three additional videos that we’ve added in question 3. Therefore, we can deduce that if we want to follow our favourite youtuber’s pattern, we shouldn’t post such short ones in the future.

Let’s begin by putting the data (the lengths of the videos) into increasing order:

	1st	2nd	3rd	4th	5th	6th
video length	8 mins	13 mins	13 mins	15 mins	23 mins	28 mins

However, we are interested not in the video lengths, but in the time it took to prepare them. The scenario says that every minute of a video requires 5 mins of editing. Therefore, every 1 min of footage will need 1 min + 5 min = 6 min in total to prepare. This means that we need to multiply the above sequence by 6:

	1st	2nd	3rd	4th	5th	6th
video length	8 min	13 min	13 min	15 min	23 min	28 min
preparation time	48 min	78 min	78 min	90 min	138 min	168 min

To draw the box-and-whiskers plot, we will need to find the 1st, 2nd, and 3rd quartile. The 2nd one is the median of our numbers, so we can use the mean median mode calculator:
(78 min + 90 min) / 2 = 84 min.
Similarly, the 1st and the 3rd quartile are the medians of the first and the second half of the sequence, respectively. Again, the calculator gives these as 78 and 138 mins, respectively.

The three quartiles that we counted above describe the box of our plot. On the other hand, the whiskers are given by the minimum and maximum values, which are 48 min and 168 min, respectively. All in all, we get the plot drawn below.

In this question, we again need to work a little with our initial data before we can calculate the answer. This is because we want to have the amount of money that each video earns us. The scenario says that every 1 min of a video means $0.20 for us, so we need to multiply the length of each video by the $0.20 per minute. This gives:

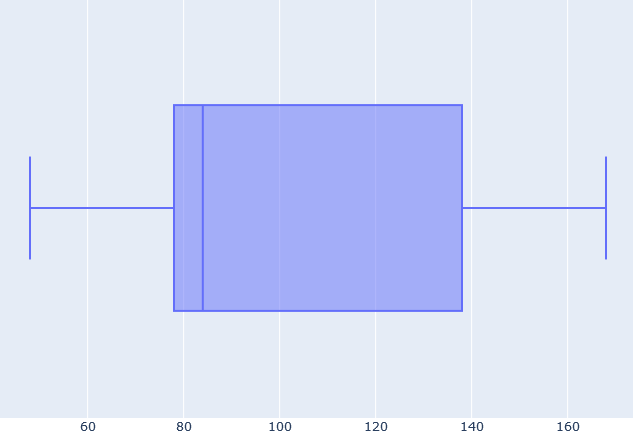
	1st	2nd	3rd	4th	5th	6th
video length	8 min	13 min	13 min	15 min	23 min	28 min
money worth	$2.60	$4.60	$3.00	$1.60	$2.60	$5.60

Well, maybe those are not big numbers, but it’s just the beginning of our career. Surely they will grow in time, right?

NOTE: Observe that this time we did not order the numbers as in Question 1. When counting the average, the variance or the standard deviation, the order of the values doesn’t matter.

Anyway, let’s see how much we’ve made per video on average. For this we will need to add all the above values and divide them by how many there are. The average calculator gives us
average₁ = ($2.60 + $4.60 + $3.00 + $1.60 + $2.60 + $5.60) / 6 ≈ $3.33.

We move on to the variance. For this, we will need to see how much each value differs from the average. This means that we need to take the money sequence and subtract from each number the average of $3.33. We obtain:

	1st	2nd	3rd	4th	5th	6th
video length	8 min	13 min	13 min	15 min	23 min	28 min
money worth	$2.60	$4.60	$3.00	$1.60	$2.60	$5.60
difference from average	-$0.73	$1.27	-$0.33	-$1.73	-$0.73	$2.27

Unfortunately, this is still not the sequence we need. We need the square of numbers we just found. We can use the exponent calculator to get approximately:

	1st	2nd	3rd	4th	5th	6th
video length	8 min	13 min	13 min	15 min	23 min	28 min
money worth	$2.60	$4.60	$3.00	$1.60	$2.60	$5.60
difference from average	-$0.73	$1.27	-$0.33	-$1.73	-$0.73	$2.27
square of difference	0.533	1.613	0.109	2.993	0.533	5.153

Now to obtain the variance, all we need is to add these values and divide them by how many there are minus 1, which is 6 – 5 = 1. In other words,
variance₁ = (0.533 + 1.613 + 0.109 + 2.993 + 0.533 + 5.153) / 5 ≈ 2.19.

Lastly, the standard deviation is the square root of the variance. Therefore, the square root calculator, or the standard deviation calculator, give:
standard_deviation₁ = √variance₁ ≈ 1.48.

We know from Question 2 how to calculate the average, the variance, and the standard deviation. The only difference now is the initial set of data. To be precise, we add the three short videos to the six we started with. Therefore, our data sequence is now
8 min, 13 min, 13 min, 15 min, 23 min, 28 min, 5 min, 7 min, 6 min.

Again, we start by translating the length of the videos to money earned:

	1st	2nd	3rd	4th	5th	6th	7th	8th	9th
video length	8 min	13 min	13 min	15 min	23 min	28 min	5 min	7 min	6 min
money worth	$2.60	$4.60	$3.00	$1.60	$2.60	$5.60	$1.00	$1.40	$1.20

Now we move on to the average. Observe that this time there are 9 numbers, so we need to divide the sum by 9 instead of 6. The average calculator gives
average₂ = ($2.60 + $4.60 + $3.00 + $1.60 + $2.60 + $5.60 + $1.00 + $1.40 + $1.20) / 9 ≈ $2.62.
Note how much the average fell when we added the three short videos.

Let’s find the variance. Firstly, we need to check how much our data differs from the mean. To do this, we subtract the mean, $2.62, from each value. We obtain:

	1st	2nd	3rd	4th	5th	6th	7th	8th	9th
video length	8 min	13 min	13 min	15 min	23 min	28 min	5 min	7 min	6 min
money worth	$2.60	$4.60	$3.00	$1.60	$2.60	$5.60	$1.00	$1.40	$1.20
difference from average	-$0.02	$1.98	$0.38	-$1.02	-$0.02	-$2.98	-$1.62	-$1.22	-$1.42

Now we square each number using the exponent calculator:

	1st	2nd	3rd	4th	5th	6th	7th	8th	9th
video length	8 min	13 min	13 min	15 min	23 min	28 min	5 min	7 min	6 min
money worth	$2.60	$4.60	$3.00	$1.60	$2.60	$5.60	$1.00	$1.40	$1.20
difference from average	-$0.02	$1.98	$0.38	-$1.02	-$0.02	-$2.98	-$1.62	-$1.22	-$1.42
square of difference	0.004	3.9204	0.1444	1.0404	0.004	8.8804	2.6244	1.4884	2.0164

And, to get the variance, we sum up these numbers and divide them by how many there are, minus one, which is 9 – 1 = 8. This gives:
variance₂ = (0.0004 + 3.9204 + 0.1444 + 1.0404 + 0.004 + 8.8804 + 2.6244 + 1.4884 + 2.0164) / 8 ≈ 2.51.

Lastly, we calculate the standard deviation using the square root calculator or the standard deviation calculator:
standard_deviation₂ = √variance₂ ≈ 1.58.

Let’s begin by putting the data (the lengths of the videos) into increasing order:

	1st	2nd	3rd	4th	5th	6th	7th
video length	20 min	21 min	22 min	22 min	24 min	26 min	35 min

Just as in question 1, we now need to find how much time it took to prepare (record and edit) the videos. This means that we need to multiply the above sequence by 6:

	1st	2nd	3rd	4th	5th	6th	7th
video length	20 min	21 min	22 min	22 min	24 min	26 min	35 min
preparation time	120 min	126 min	132 min	132 min	144 min	156 min	210 min

Recall that to draw the box-and-whiskers plot, we will need to find the 1st, 2nd, and 3rd quartile. The 2nd one is the median of our numbers, so we can use the mean median mode calculator to find that it is the middle number in our sequence: 132 min.

Similarly, the 1st and the 3rd quartile are the medians of the first and the second half of the sequence, respectively. Again, the calculator gives these as
(132 min + 126 min) / 2 = 129 min
and
(144 min + 156 min) / 2 = 150 min,
respectively.

The three quartiles that we counted above describe the box of our plot. On the other hand, the whiskers are given by the minimum and maximum values, which are 120 min and 210 min, respectively. All in all, we get the plot drawn below.