Concepts addressed: percentages, trigonometry, unit conversion, velocity calculation.
Recommended grade: 11th.
Difficulty level: Advanced.
A basic version of Mountain trip is also available.
Scenario:
Winter break is here, and you’re planning a trip to the mountains for a few days with three friends. The cabin you’ll be staying at is a hundred miles away, so you decide to make it a road trip and go there by car, travelling at 60mph on average.
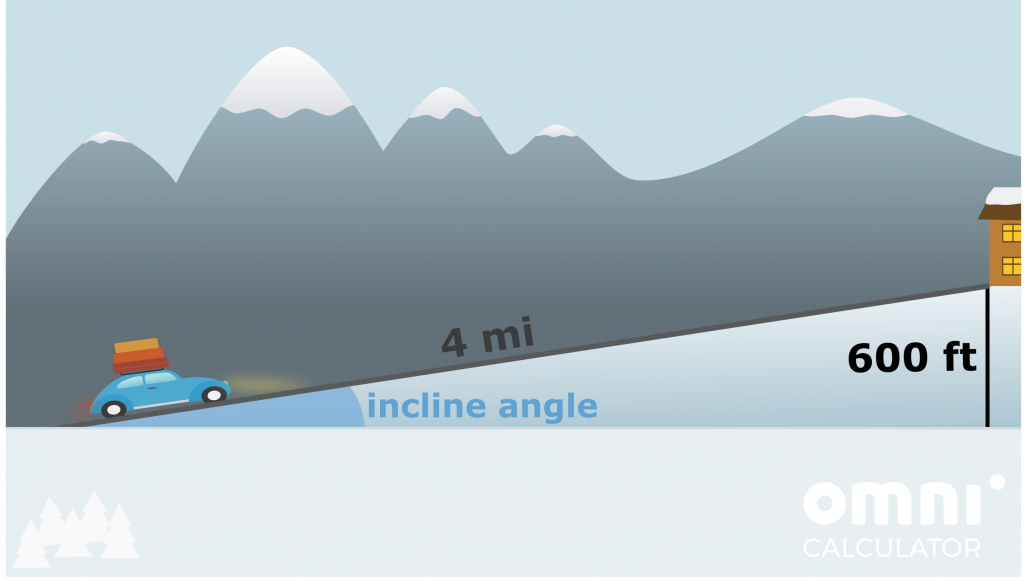
- The cabin has an altitude of 600 feet above sea level. Assuming that you begin at sea level, start driving uphill four miles away from destination, and the slope is constant, what will the angle of incline be?

- When you get close to the destination, it turns out that the last thousand feet of the path are inaccessible by car, and you have to walk. Assuming your walking speed with the bags is 3 mph, how long will the walk take? How did the time of the whole trip change from what was expected initially, expressed as a percentage?
Useful calculators:
- Speed calculator – https://www.omnicalculator.com/everyday-life/speed
- Percentage calculator – https://www.omnicalculator.com/math/percentage
- Conversion calculator – https://www.omnicalculator.com/conversion/conversion-calculator
- Arcsin calculator – https://www.omnicalculator.com/math/arcsin
- Slope calculator – https://www.omnicalculator.com/math/slope
Question 1 hints:
Question 2 hints:
Solutions:
Step-by-step solution:
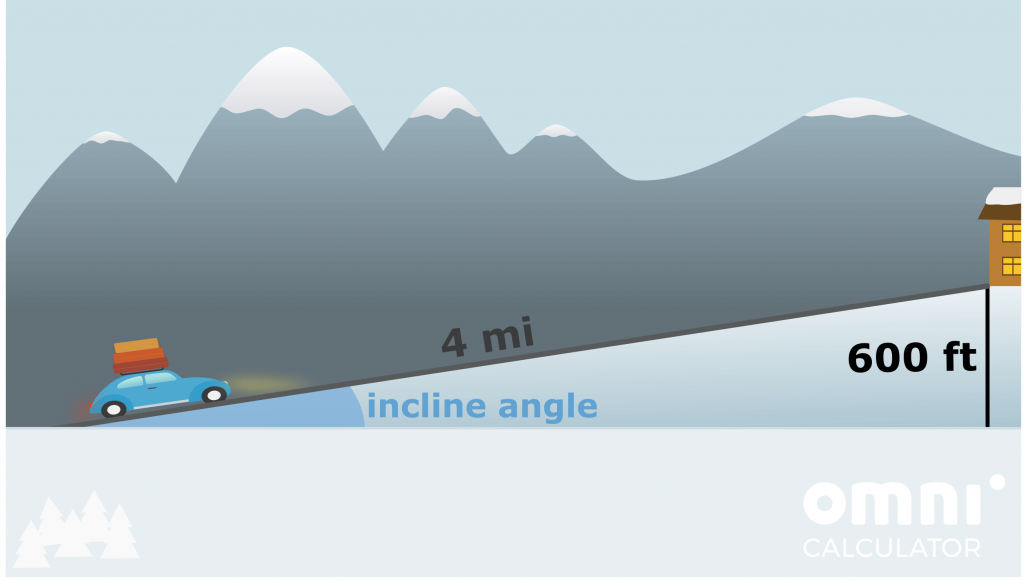
Remember that, to not make any mistakes, we need to make sure all of our units are the same. This means that we need to change the miles to feet (or vice versa). The conversion calculator gives c = 4 mi = 21,120 ft. As we are dealing with the hypotenuse and the opposite side, SOHCAHTOA tells use we need to use the sin function (note that arcsin = sin-1):
angle = arcsin(a / c) = arcsin(600 ft / 21,120 ft) ≈ 1.6 deg.
We can use the slope calculator to check our result.
Observe that the incline angle is in fact the arcsin of the fraction given by the triangle’s sides. Therefore, we could have also used the arcsin calculator.
t_expected = s / v = 100 mi / 60 mph = 1 2/3 hr.

Now let’s see how much time the trip took in reality. It is essential here to have a good understanding of the situation we are faced with: the 100-mile section of the road is now divided into two parts. The first one contains all of it, except for the last 1,000 ft, and we can cover that part at 60 mph. The second is the unfortunate last 1,000 ft that we’re forced to walk at the speed of 3 mph. This allows us to separate the situation into two sets: s₁ = 100 mi – 1,000 ft and v₁ = 60 mph, and s₂ = 1,000 ft and v₂ = 3 mph, for the first part and second part respectively.
Before we start calculations, we need everything in the same units, i.e., we need to change feet into miles. The conversion calculator gives
s₁ = 100 mi – 1,000 ft = 100 mi – 0.1894 mi ≈ 99.81 mi,
s₂ = 1,000 ft ≈ 0.19 mi.
Now we are ready to find the time both parts of the trip took. The speed calculator gives
t₁ = s₁ / v₁ ≈ 99.81 mi / 60 mph ≈ 1.664 hr,
t₂ = s₂ / v₂ ≈ 0.19 mi / 3 mph ≈ 0.063 hr.
Therefore, the actual time of the trip is
t_actual = t₁ + t₂ ≈ 1.664 hr + 0.063 hr = 1.727 hr.
This, in turn, means that it took
difference = t_actual – t_expected ≈ 1 2/3 hr – 1.727 hr ≈ 0.06 hr
longer than we had hoped for.
We are left with the problem of presenting this time difference as a percentage of what we expected the trip to take. Note that we wish to get the increase with respect to the number where we drove the whole way. Therefore, the percentage calculator tell us that our final answer is:
increase = (difference / t_expected) * 100% = (0.06 hr / 5/3 hr) * 100% = 3.6%.