Concepts addressed: percentages, rectangular prism volume, rectangular prism area, unit conversion, square area.
Recommended grade: 7th.
Difficulty level: Basic.
An advanced version of Building a swimming pool is also available.
Scenario:
This is the year – you’re finally building an in-ground swimming pool in your backyard! You can already see all the envious faces, but first someone’s got to do the dirty work.
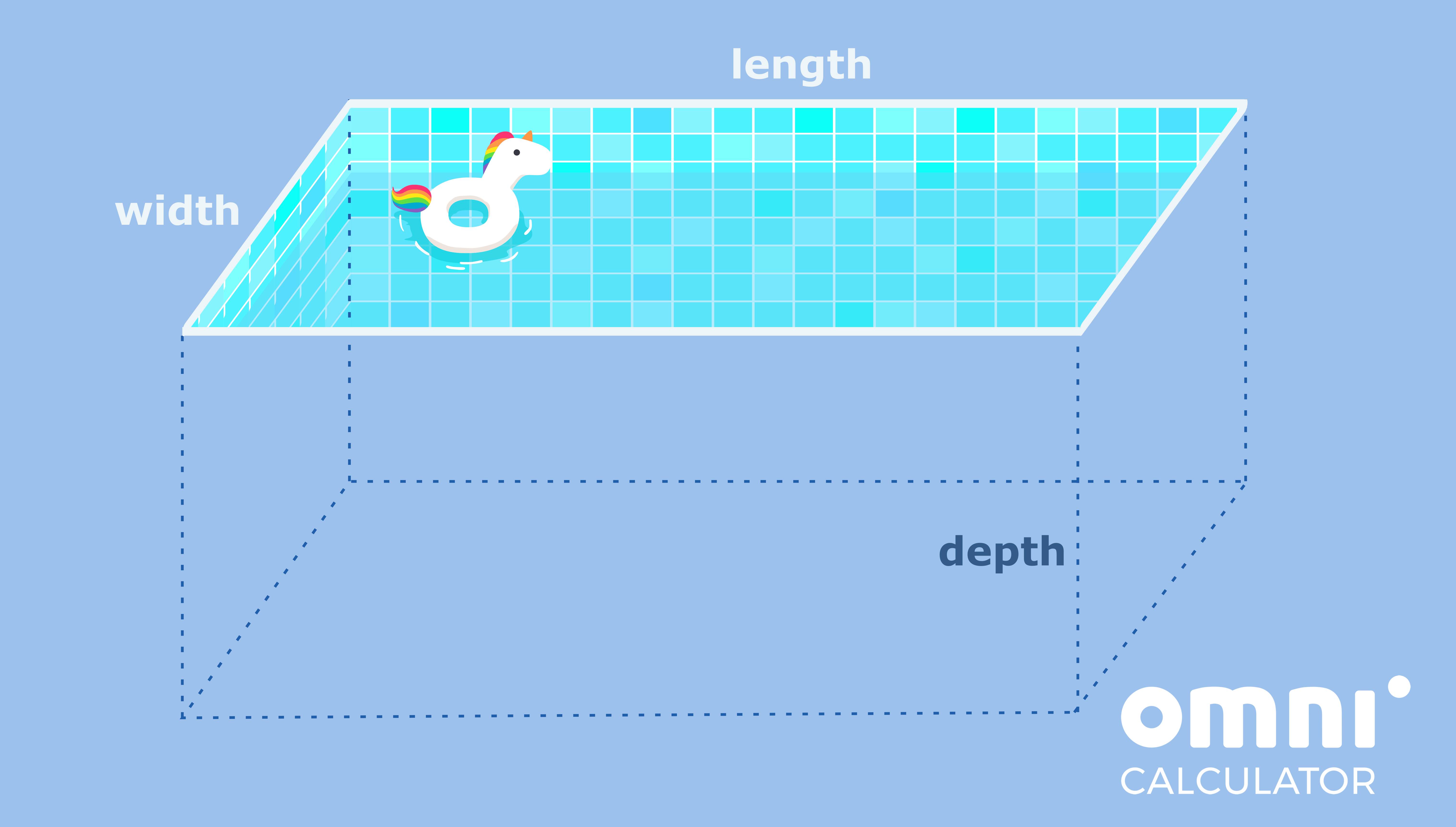
- You’ve decided the pool should be rectangular, with dimension eight by thirteen feet and as deep as you are tall. How much water will you need for it?

- You want to tile the inside of the pool with square eight by eight-inch tiles. How many of those will you need? Better buy 5% more in case some of them break in the process.
- A pack of ten tiles costs $15, and you get $50 allowance every week. How long will it take to save for them if you already have $80 saved, and you’ll be putting all your allowance towards it?
Useful calculators:
- Rectangular prism calculator – https://www.omnicalculator.com/math/rectangular-prism
- Volume calculator – https://www.omnicalculator.com/math/volume
- Percentage calculator – https://www.omnicalculator.com/math/percentage
- Area of a square calculator – https://www.omnicalculator.com/math/square-area
- Conversion calculator – https://www.omnicalculator.com/conversion/conversion-calculator
Question 1 hints:
Question 2 hints:
Question 3 hints:
Solutions (WARNING: depend on the height, example for height being 6 feet):
Step-by-step solution:
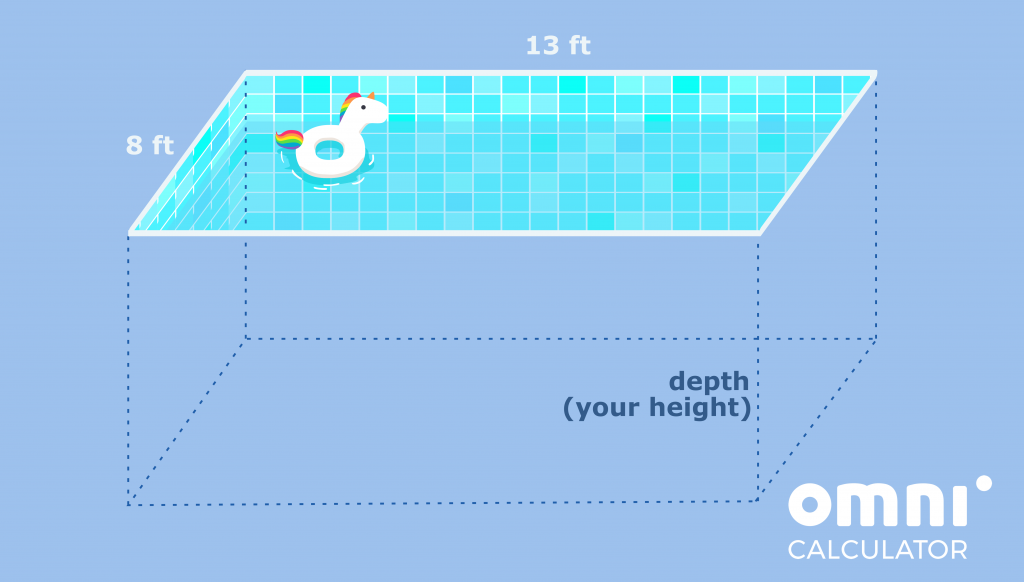
This gives us all the information we need to calculate the volume with the rectangular prism calculator:
V = a * b * h = 8 ft * 13 ft * 6 ft = 624 ft³.
A = base_area + lateral_area = a * b + 2 * a * h + 2 * b * h = 8 ft * 13 ft + 2 * 8 ft * 6 ft + 2 * 13 ft * 6 ft = 356 ft².
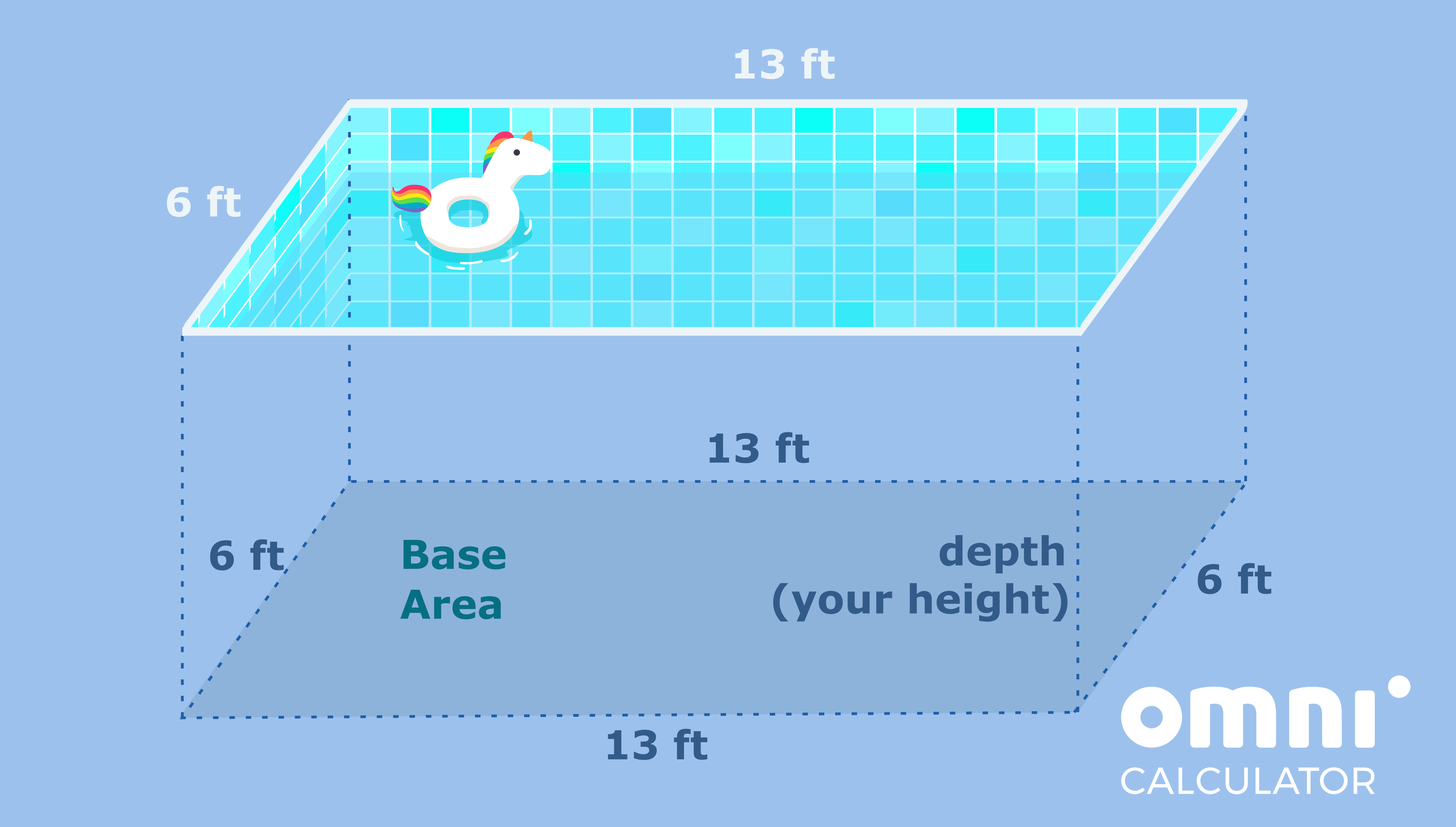
Now that we know how much area we’re working with, we need to find the number of tiles that will tile it. A single tile is a square of side 8 in. For our calculations, we need the units to agree, so let’s use the conversion calculator to write the tile side in feet: a_tile = 8 in = 2/3 ft. Therefore, the area of a square calculator states that a single tile has an area of:
A_tile = (a_tile)² = (2/3 ft)² = 4/9 ft².
Therefore, we’ll need:
A / A_tile = 356 ft² / (4/9 ft²) = 801
tiles to cover the whole area.
Lastly, we need to add to that number the additional 5% in case some of the tiles break. If we want to buy 5% more than what is required, then this means that we need 100% + 5% = 105% of what we calculated above. According to the percentage calculator, this is 105% * 801 = 841.05, which tells us that we need to buy 842 tiles.
NOTE: If you’ve rounded the area of a single tile to 0.44 ft² instead of keeping it as a fraction, then you could have gotten a slightly different result. You can see that in the above calculations, there is no approximation anywhere, which from the point of view of real-life scenarios, is a great thing. However, in many cases, rounding numbers is very useful. As a general tip to avoid large discrepancy we suggest doing them as late as possible.
cost = 85 * pack_cost = 85 * $15 = $1,275.
Now let’s subtract from that the amount you’ve already saved to get how much we still need:
money_needed = cost – money_saved = $1,275 – $80 = $1,195.
Lastly, we must see how many allowances (and therefore weeks) it will take to save such a sum. Since we get $50 every week, we need 1,195 / 50 = 23.9, or rather 24 weeks to get that much money. But summer will be over in 24 weeks!
Oh well, maybe next year will be the year?